Plotting two simple sine functions¶
A simple example plotting a fit of two sine functions.
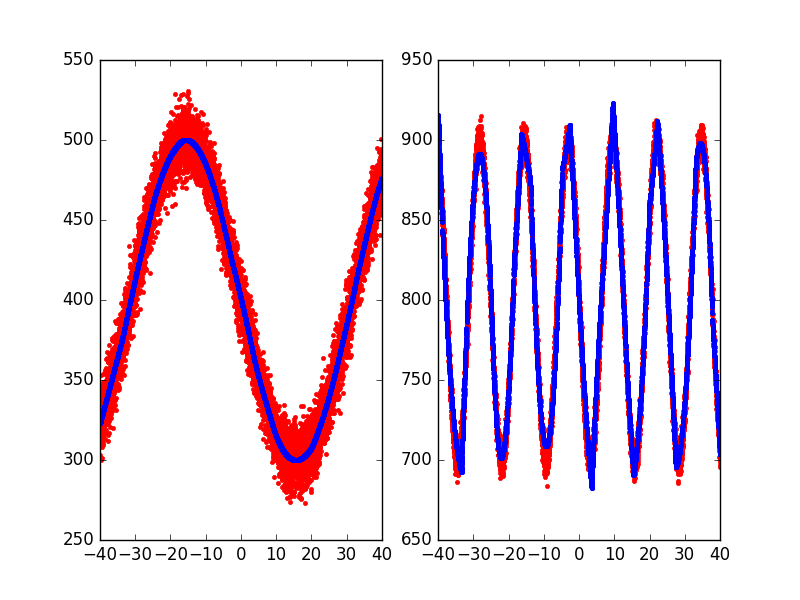
Out:
Forward Pass
---------------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
---------------------------------------------------------------------
0 - - - 4718.876841 1 4719.821 0.000 0.000
1 0 6 3411 3982.618784 3 3987.402 0.156 0.155
2 1 6 7550 2563.588158 5 2569.237 0.457 0.456
3 2 6 2668 2078.056464 7 2084.722 0.560 0.558
4 4 6 8256 1852.024839 9 1859.828 0.608 0.606
5 1 6 6806 1504.833192 11 1512.689 0.681 0.680
6 3 6 4950 873.297723 13 878.737 0.815 0.814
7 0 6 6442 475.741749 15 479.186 0.899 0.898
8 13 6 9729 338.281631 17 341.073 0.928 0.928
9 10 6 4788 276.828324 19 279.393 0.941 0.941
10 14 6 716 180.664061 21 182.521 0.962 0.961
11 9 6 9876 138.935606 23 140.505 0.971 0.970
12 14 6 1513 119.120070 25 120.587 0.975 0.974
13 20 6 4077 100.226223 27 101.562 0.979 0.978
14 23 6 1737 87.489761 29 88.745 0.981 0.981
15 15 6 2485 83.930788 31 85.221 0.982 0.982
---------------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Pruning Pass
--------------------------------------------------
iter bf terms mse gcv rsq grsq
--------------------------------------------------
0 - 31 83.97 85.261 0.982 0.982
1 6 30 83.97 85.219 0.982 0.982
2 23 29 83.97 85.176 0.982 0.982
3 10 28 83.97 85.133 0.982 0.982
4 1 27 83.96 85.081 0.982 0.982
5 13 26 83.97 85.047 0.982 0.982
6 27 25 84.08 85.119 0.982 0.982
7 24 24 84.17 85.162 0.982 0.982
8 16 23 84.59 85.547 0.982 0.982
9 29 22 86.29 87.220 0.982 0.982
10 30 21 88.03 88.935 0.981 0.981
11 14 20 109.08 110.150 0.977 0.977
12 8 19 110.96 111.984 0.976 0.976
13 22 18 111.30 112.274 0.976 0.976
14 2 17 122.48 123.488 0.974 0.974
15 11 16 142.15 143.254 0.970 0.970
16 17 15 181.40 182.717 0.962 0.961
17 28 14 246.99 248.655 0.948 0.947
18 21 13 305.08 306.979 0.935 0.935
19 4 12 426.20 428.636 0.910 0.909
20 18 11 577.60 580.611 0.878 0.877
21 15 10 842.68 846.653 0.821 0.821
22 19 9 948.10 952.090 0.799 0.798
23 12 8 1384.27 1389.410 0.707 0.706
24 25 7 1976.05 1982.387 0.581 0.580
25 26 6 2322.66 2328.944 0.508 0.507
26 5 5 2546.36 2551.967 0.460 0.459
27 7 4 2885.90 2890.817 0.388 0.388
28 20 3 3228.56 3232.442 0.316 0.315
29 3 2 4651.66 4654.922 0.014 0.014
30 9 1 4718.88 4719.821 0.000 0.000
--------------------------------------------------
Selected iteration: 0
Earth Model
-----------------------------------------------------------------------------------
Basis Function Pruned Coefficient 0 Coefficient 1
-----------------------------------------------------------------------------------
(Intercept) No 0.887775 4.96805
h(x6+24.7123) No 0.246346 -1.19494
h(-24.7123-x6) No -22.3647 -125.569
h(x6-9.54303)*h(x6+24.7123) No -0.885912 5.25986
h(9.54303-x6)*h(x6+24.7123) No 0.988511 -2.2644
h(x6+33.3795)*h(-24.7123-x6) No -0.0757852 17.9857
h(-33.3795-x6)*h(-24.7123-x6) No 0.318799 -8.75475
h(x6+18.4449)*h(9.54303-x6)*h(x6+24.7123) No 0.00339884 -0.179754
h(-18.4449-x6)*h(9.54303-x6)*h(x6+24.7123) No -0.00131486 0.0186784
h(x6+2.68533)*h(x6+24.7123) No 0.649813 -2.59934
h(-2.68533-x6)*h(x6+24.7123) No -0.488166 4.48859
h(x6-19.9252)*h(x6-9.54303)*h(x6+24.7123) No 0.0188511 -0.0708319
h(19.9252-x6)*h(x6-9.54303)*h(x6+24.7123) No -0.015557 -0.0259405
h(x6-27.4138) No -23.4906 -129.961
h(27.4138-x6) No 0.174544 4.62948
h(x6-33.0979)*h(x6-27.4138) No -1.84708 -6.64501
h(33.0979-x6)*h(x6-27.4138) No 1.49611 -3.91794
h(x6+16.3674)*h(-2.68533-x6)*h(x6+24.7123) No 0.000453922 -0.144786
h(-16.3674-x6)*h(-2.68533-x6)*h(x6+24.7123) No -0.00748619 -0.291898
h(x6+4.82217)*h(27.4138-x6) No 0.342173 12.2396
h(-4.82217-x6)*h(27.4138-x6) No -0.348983 -11.4899
h(x6-22.205)*h(x6+2.68533)*h(x6+24.7123) No 0.00262249 0.0520941
h(22.205-x6)*h(x6+2.68533)*h(x6+24.7123) No -0.00321566 -0.102549
h(x6-3.57421)*h(27.4138-x6) No -0.188022 -7.83165
h(3.57421-x6)*h(27.4138-x6) No 0.586357 7.30971
h(x6+13.8327)*h(-4.82217-x6)*h(27.4138-x6) No 0.00403765 -0.311882
h(-13.8327-x6)*h(-4.82217-x6)*h(27.4138-x6) No -0.0044294 0.147935
h(x6-15.439)*h(x6-3.57421)*h(27.4138-x6) No 0.0289558 -0.0268093
h(15.439-x6)*h(x6-3.57421)*h(27.4138-x6) No -0.0284085 0.321538
h(x6-37.8181)*h(x6-33.0979)*h(x6-27.4138) No -0.0431023 0.228017
h(37.8181-x6)*h(x6-33.0979)*h(x6-27.4138) No 0.026043 0.495148
-----------------------------------------------------------------------------------
MSE: 83.9704, GCV: 85.2615, RSQ: 0.9822, GRSQ: 0.9819
import numpy
import matplotlib.pyplot as plt
from pyearth import Earth
# Create some fake data
numpy.random.seed(2)
m = 10000
n = 10
X = 80 * numpy.random.uniform(size=(m, n)) - 40
y1 = 100 * \
numpy.abs(numpy.sin((X[:, 6]) / 10) - 4.0) + \
10 * numpy.random.normal(size=m)
y2 = 100 * \
numpy.abs(numpy.sin((X[:, 6]) / 2) - 8.0) + \
5 * numpy.random.normal(size=m)
# Fit an Earth model
model = Earth(max_degree=3, minspan_alpha=.5)
y_mix = numpy.concatenate((y1[:, numpy.newaxis], y2[:, numpy.newaxis]), axis=1)
model.fit(X, y_mix)
# Print the model
print(model.trace())
print(model.summary())
# Plot the model
y_hat = model.predict(X)
fig = plt.figure()
ax = fig.add_subplot(1, 2, 1)
ax.plot(X[:, 6], y_mix[:, 0], 'r.')
ax.plot(X[:, 6], model.predict(X)[:, 0], 'b.')
ax = fig.add_subplot(1, 2, 2)
ax.plot(X[:, 6], y_mix[:, 1], 'r.')
ax.plot(X[:, 6], model.predict(X)[:, 1], 'b.')
plt.show()
Total running time of the script: (0 minutes 28.061 seconds)
Download Python source code:
plot_sine_wave_2d.py
Download IPython notebook:
plot_sine_wave_2d.ipynb