Plotting feature importance¶
A simple example showing how to compute and display feature importances, it is also compared with the feature importances obtained using random forests.
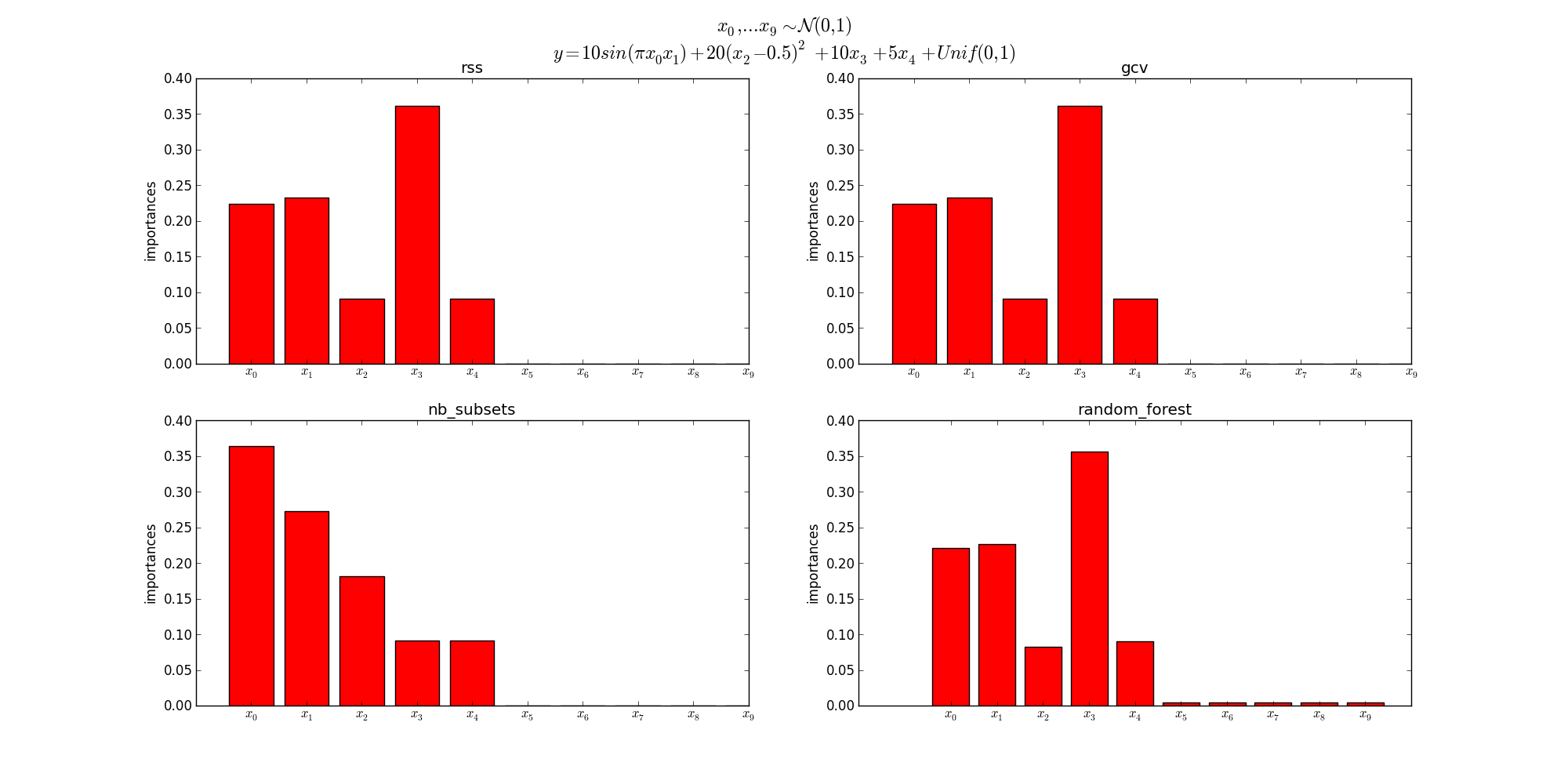
Feature importance is a measure of the effect of the features on the outputs. For each feature, the values go from 0 to 1 where a higher the value means that the feature will have a higher effect on the outputs.
Currently three criteria are supported : ‘gcv’, ‘rss’ and ‘nb_subsets’. See [1], section 12.3 for more information about the criteria.
| [1] | http://www.milbo.org/doc/earth-notes.pdf |
Out:
Beginning forward pass
-----------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
-----------------------------------------------------------------
0 - - - 24.101072 1 24.106 0.000 0.000
1 0 3 -1 15.626212 2 15.637 0.352 0.351
2 0 1 2446 10.884011 4 10.903 0.548 0.548
3 0 0 43 6.386236 6 6.404 0.735 0.734
4 0 2 3272 4.226153 8 4.242 0.825 0.824
5 0 4 -1 2.136919 9 2.146 0.911 0.911
6 4 1 9815 1.113502 11 1.119 0.954 0.954
---------------------------------------------------------------
Stopping Condition 0: Reached maximum number of terms
Beginning pruning pass
--------------------------------------------
iter bf terms mse gcv rsq grsq
--------------------------------------------
0 - 11 1.11 1.119 0.954 0.954
1 2 10 1.40 1.405 0.942 0.942
2 10 9 1.63 1.635 0.932 0.932
3 4 8 1.68 1.684 0.930 0.930
4 9 7 2.16 2.168 0.910 0.910
5 6 6 3.84 3.851 0.841 0.840
6 7 5 4.29 4.297 0.822 0.822
7 8 4 6.41 6.425 0.734 0.733
8 5 3 10.89 10.907 0.548 0.548
9 3 2 15.63 15.637 0.352 0.351
10 1 1 24.10 24.106 -0.000 -0.000
------------------------------------------------
Selected iteration: 0
Forward Pass
-----------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
-----------------------------------------------------------------
0 - - - 24.101072 1 24.106 0.000 0.000
1 0 3 -1 15.626212 2 15.637 0.352 0.351
2 0 1 2446 10.884011 4 10.903 0.548 0.548
3 0 0 43 6.386236 6 6.404 0.735 0.734
4 0 2 3272 4.226153 8 4.242 0.825 0.824
5 0 4 -1 2.136919 9 2.146 0.911 0.911
6 4 1 9815 1.113502 11 1.119 0.954 0.954
-----------------------------------------------------------------
Stopping Condition 0: Reached maximum number of terms
Pruning Pass
------------------------------------------------
iter bf terms mse gcv rsq grsq
------------------------------------------------
0 - 11 1.11 1.119 0.954 0.954
1 2 10 1.40 1.405 0.942 0.942
2 10 9 1.63 1.635 0.932 0.932
3 4 8 1.68 1.684 0.930 0.930
4 9 7 2.16 2.168 0.910 0.910
5 6 6 3.84 3.851 0.841 0.840
6 7 5 4.29 4.297 0.822 0.822
7 8 4 6.41 6.425 0.734 0.733
8 5 3 10.89 10.907 0.548 0.548
9 3 2 15.63 15.637 0.352 0.351
10 1 1 24.10 24.106 -0.000 -0.000
------------------------------------------------
Selected iteration: 0
Earth Model
----------------------------------------------------
Basis Function Pruned Coefficient
----------------------------------------------------
(Intercept) No 7.68887
x3 No 10.0005
h(x1-0.525027) No 5.34483
h(0.525027-x1) No -9.90971
h(x0-0.563426) No 10.4923
h(0.563426-x0) No -12.0495
h(x2-0.496723) No 9.90482
h(0.496723-x2) No 10.1095
x4 No 5.00753
h(x1-0.496528)*h(x0-0.563426) No -56.5856
h(0.496528-x1)*h(x0-0.563426) No -36.1381
----------------------------------------------------
MSE: 1.1135, GCV: 1.1193, RSQ: 0.9538, GRSQ: 0.9536
nb_subsets gcv rss
x3 0.09 0.36 0.36
x1 0.27 0.23 0.23
x0 0.36 0.22 0.22
x2 0.18 0.09 0.09
x4 0.09 0.09 0.09
x9 0.00 0.00 0.00
x8 0.00 0.00 0.00
x7 0.00 0.00 0.00
x6 0.00 0.00 0.00
x5 0.00 0.00 0.00
import numpy
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from pyearth import Earth
# Create some fake data
numpy.random.seed(2)
m = 10000
n = 10
X = numpy.random.uniform(size=(m, n))
y = (10 * numpy.sin(numpy.pi * X[:, 0] * X[:, 1]) +
20 * (X[:, 2] - 0.5) ** 2 +
10 * X[:, 3] +
5 * X[:, 4] + numpy.random.uniform(size=m))
# Fit an Earth model
criteria = ('rss', 'gcv', 'nb_subsets')
model = Earth(max_degree=3,
max_terms=10,
minspan_alpha=.5,
feature_importance_type=criteria,
verbose=True)
model.fit(X, y)
rf = RandomForestRegressor()
rf.fit(X, y)
# Print the model
print(model.trace())
print(model.summary())
print(model.summary_feature_importances(sort_by='gcv'))
# Plot the feature importances
importances = model.feature_importances_
importances['random_forest'] = rf.feature_importances_
criteria = criteria + ('random_forest',)
idx = 1
fig = plt.figure(figsize=(20, 10))
labels = ['$x_{}$'.format(i) for i in range(n)]
for crit in criteria:
plt.subplot(2, 2, idx)
plt.bar(numpy.arange(len(labels)),
importances[crit],
align='center',
color='red')
plt.xticks(numpy.arange(len(labels)), labels)
plt.title(crit)
plt.ylabel('importances')
idx += 1
title = '$x_0,...x_9 \sim \mathcal{N}(0, 1)$\n$y= 10sin(\pi x_{0}x_{1}) + 20(x_2 - 0.5)^2 + 10x_3 + 5x_4 + Unif(0, 1)$'
fig.suptitle(title, fontsize="x-large")
plt.show()
Total running time of the script: (0 minutes 1.583 seconds)
Download Python source code:
plot_feature_importance.py
Download IPython notebook:
plot_feature_importance.ipynb