Plotting a multicolumn regression problem that includes missingness¶
An example plotting a simultaneous fit of the sine and cosine functions. There are two redundant predictors, each of which has independent and random missingness.
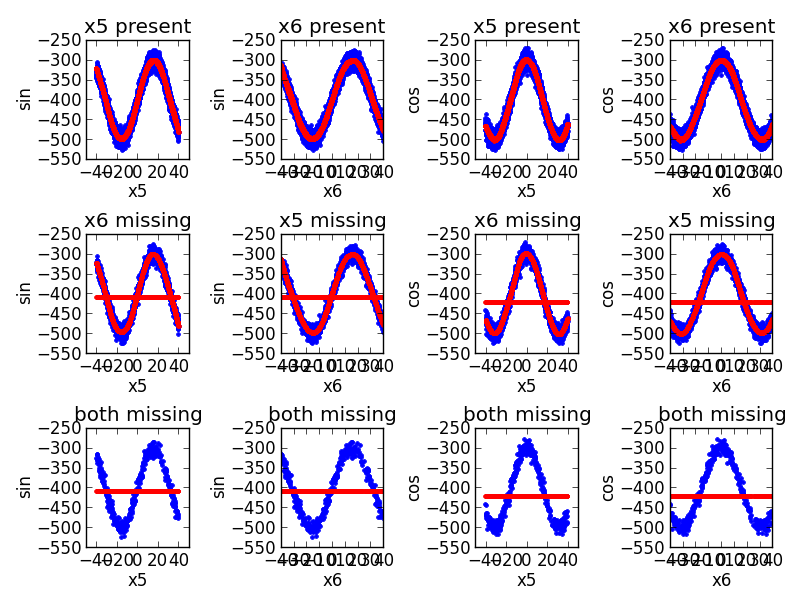
Out:
Beginning forward pass
---------------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
---------------------------------------------------------------------
0 - - - 4893.487156 1 4894.466 0.000 0.000
1 0 6 2137 2847.258070 5 2853.532 0.418 0.417
2 3 6 1882 1604.248646 7 1609.395 0.672 0.671
3 4 6 3981 1091.498983 9 1096.098 0.777 0.776
4 0 5 3872 865.753079 13 871.146 0.823 0.822
5 1 5 6251 677.545451 17 683.136 0.862 0.860
6 11 5 7295 529.897093 19 534.806 0.892 0.891
7 3 5 1687 429.659153 23 434.512 0.912 0.911
8 12 5 8217 356.980379 25 361.376 0.927 0.926
9 12 6 6100 311.466783 29 315.937 0.936 0.935
10 23 5 7367 305.774544 31 310.476 0.938 0.937
11 5 6 3688 302.715204 33 307.679 0.938 0.937
-------------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Beginning pruning pass
------------------------------------------------
iter bf terms mse gcv rsq grsq
------------------------------------------------
0 - 33 302.73 307.691 0.938 0.937
1 2 32 302.73 307.536 0.938 0.937
2 12 31 302.73 307.381 0.938 0.937
3 13 30 302.73 307.226 0.938 0.937
4 3 29 302.71 307.058 0.938 0.937
5 10 28 302.73 306.917 0.938 0.937
6 16 27 302.83 306.872 0.938 0.937
7 30 26 303.00 306.881 0.938 0.937
8 32 25 303.26 306.990 0.938 0.937
9 15 24 303.80 307.382 0.938 0.937
10 25 23 305.32 308.772 0.938 0.937
11 1 22 306.62 309.932 0.937 0.937
12 31 21 309.57 312.748 0.937 0.936
13 29 20 314.07 317.136 0.936 0.935
14 19 19 322.35 325.336 0.934 0.934
15 22 18 337.54 340.500 0.931 0.930
16 6 17 347.58 350.448 0.929 0.928
17 28 16 361.15 363.944 0.926 0.926
18 24 15 371.25 373.935 0.924 0.924
19 27 14 439.31 442.265 0.910 0.910
20 7 13 465.62 468.521 0.905 0.904
21 21 12 570.82 574.085 0.883 0.883
22 5 11 613.94 617.143 0.875 0.874
23 18 10 766.50 770.116 0.843 0.843
24 8 9 941.18 945.144 0.808 0.807
25 14 8 1153.75 1158.031 0.764 0.763
26 9 7 1376.30 1380.712 0.719 0.718
27 17 6 1780.93 1785.752 0.636 0.635
28 20 5 2192.81 2197.638 0.552 0.551
29 26 4 2561.68 2566.044 0.477 0.476
30 11 3 3302.02 3305.984 0.325 0.325
31 4 2 3745.34 3747.962 0.235 0.234
32 23 1 4893.49 4894.466 0.000 0.000
--------------------------------------------------
Selected iteration: 0
Forward Pass
---------------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
---------------------------------------------------------------------
0 - - - 4893.487156 1 4894.466 0.000 0.000
1 0 6 2137 2847.258070 5 2853.532 0.418 0.417
2 3 6 1882 1604.248646 7 1609.395 0.672 0.671
3 4 6 3981 1091.498983 9 1096.098 0.777 0.776
4 0 5 3872 865.753079 13 871.146 0.823 0.822
5 1 5 6251 677.545451 17 683.136 0.862 0.860
6 11 5 7295 529.897093 19 534.806 0.892 0.891
7 3 5 1687 429.659153 23 434.512 0.912 0.911
8 12 5 8217 356.980379 25 361.376 0.927 0.926
9 12 6 6100 311.466783 29 315.937 0.936 0.935
10 23 5 7367 305.774544 31 310.476 0.938 0.937
11 5 6 3688 302.715204 33 307.679 0.938 0.937
---------------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Pruning Pass
--------------------------------------------------
iter bf terms mse gcv rsq grsq
--------------------------------------------------
0 - 33 302.73 307.691 0.938 0.937
1 2 32 302.73 307.536 0.938 0.937
2 12 31 302.73 307.381 0.938 0.937
3 13 30 302.73 307.226 0.938 0.937
4 3 29 302.71 307.058 0.938 0.937
5 10 28 302.73 306.917 0.938 0.937
6 16 27 302.83 306.872 0.938 0.937
7 30 26 303.00 306.881 0.938 0.937
8 32 25 303.26 306.990 0.938 0.937
9 15 24 303.80 307.382 0.938 0.937
10 25 23 305.32 308.772 0.938 0.937
11 1 22 306.62 309.932 0.937 0.937
12 31 21 309.57 312.748 0.937 0.936
13 29 20 314.07 317.136 0.936 0.935
14 19 19 322.35 325.336 0.934 0.934
15 22 18 337.54 340.500 0.931 0.930
16 6 17 347.58 350.448 0.929 0.928
17 28 16 361.15 363.944 0.926 0.926
18 24 15 371.25 373.935 0.924 0.924
19 27 14 439.31 442.265 0.910 0.910
20 7 13 465.62 468.521 0.905 0.904
21 21 12 570.82 574.085 0.883 0.883
22 5 11 613.94 617.143 0.875 0.874
23 18 10 766.50 770.116 0.843 0.843
24 8 9 941.18 945.144 0.808 0.807
25 14 8 1153.75 1158.031 0.764 0.763
26 9 7 1376.30 1380.712 0.719 0.718
27 17 6 1780.93 1785.752 0.636 0.635
28 20 5 2192.81 2197.638 0.552 0.551
29 26 4 2561.68 2566.044 0.477 0.476
30 11 3 3302.02 3305.984 0.325 0.325
31 4 2 3745.34 3747.962 0.235 0.234
32 23 1 4893.49 4894.466 0.000 0.000
--------------------------------------------------
Selected iteration: 0
Earth Model
---------------------------------------------------------------------------------------------------------------------------------------------------------------
Basis Function Pruned Coefficient 0 Coefficient 1
---------------------------------------------------------------------------------------------------------------------------------------------------------------
(Intercept) No -5.32206e+09 1.19712e+10
present(x6) No 1.93529e+09 -4.35316e+09
missing(x6) No 2.90294e+09 -6.52973e+09
C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No 3.39758 -5.46026
C(x6|s=-1,-13.0806,-0.196727,11.4609)*present(x6) No -1.66364 -10.5413
C(x6|s=+1,11.4609,23.1185,23.8585)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No -0.425959 0.166173
C(x6|s=-1,11.4609,23.1185,23.8585)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No 0.388521 -0.0691114
C(x6|s=+1,-32.9814,-25.9644,-13.0806)*C(x6|s=-1,-13.0806,-0.196727,11.4609)*present(x6) No -0.481603 -0.0625639
C(x6|s=-1,-32.9814,-25.9644,-13.0806)*C(x6|s=-1,-13.0806,-0.196727,11.4609)*present(x6) No 0.26819 0.319225
present(x5) No 2.41912e+09 -5.44144e+09
missing(x5) No 2.41912e+09 -5.44144e+09
C(x5|s=+1,-9.38452,1.36818,14.8996)*present(x5) No 0.121137 -10.2913
C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No -2.91523 -0.483027
present(x5)*present(x6) No 9.67647e+08 -2.17658e+09
missing(x5)*present(x6) No 9.67647e+08 -2.17658e+09
C(x5|s=+1,-19.348,1.389,13.869)*present(x5)*present(x6) No -5.21392 6.62229
C(x5|s=-1,-19.348,1.389,13.869)*present(x5)*present(x6) No 9.22985 -6.41773
C(x5|s=+1,14.8996,28.4311,34.2832)*C(x5|s=+1,-9.38452,1.36818,14.8996)*present(x5) No -0.229284 0.365081
C(x5|s=-1,14.8996,28.4311,34.2832)*C(x5|s=+1,-9.38452,1.36818,14.8996)*present(x5) No 0.444821 -0.129529
present(x5)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No 3.81312 -0.595014
missing(x5)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No -0.416023 -4.86417
C(x5|s=+1,13.869,26.349,33.2422)*present(x5)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No 0.247209 -0.335965
C(x5|s=-1,13.869,26.349,33.2422)*present(x5)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No -0.42469 0.0927334
C(x5|s=+1,-35.584,-31.0829,-25.61)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No -0.417321 -0.122234
C(x5|s=-1,-35.584,-31.0829,-25.61)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No 0.199904 0.309103
present(x6)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No -5.554 7.50276
missing(x6)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No 2.63895 -7.98618
C(x6|s=+1,-35.0155,-30.0326,4.9814)*present(x6)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No 0.434228 0.0633731
C(x6|s=-1,-35.0155,-30.0326,4.9814)*present(x6)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No -0.266897 -0.316667
C(x5|s=+1,-25.61,-20.1372,-9.38452)*C(x5|s=+1,-35.584,-31.0829,-25.61)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No 0.0011487 0.00313568
C(x5|s=-1,-25.61,-20.1372,-9.38452)*C(x5|s=+1,-35.584,-31.0829,-25.61)*C(x5|s=-1,-9.38452,1.36818,14.8996)*present(x5) No -0.00453544 -0.00781131
C(x6|s=+1,23.8585,24.5984,32.2969)*C(x6|s=+1,11.4609,23.1185,23.8585)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No 0.00825191 0.00633597
C(x6|s=-1,23.8585,24.5984,32.2969)*C(x6|s=+1,11.4609,23.1185,23.8585)*C(x6|s=+1,-13.0806,-0.196727,11.4609)*present(x6) No -0.0136051 -0.00110534
---------------------------------------------------------------------------------------------------------------------------------------------------------------
MSE: 296.2991, GCV: 301.1581, RSQ: 0.9395, GRSQ: 0.9385
import numpy
import matplotlib.pyplot as plt
from pyearth import Earth
# Create some fake data
numpy.random.seed(2)
m = 10000
n = 10
X = 80 * numpy.random.uniform(size=(m, n)) - 40
X[:, 5] = X[:, 6] + numpy.random.normal(0, .1, m)
y1 = 100 * \
(numpy.sin((X[:, 5] + X[:, 6]) / 20) - 4.0) + \
10 * numpy.random.normal(size=m)
y2 = 100 * \
(numpy.cos((X[:, 5] + X[:, 6]) / 20) - 4.0) + \
10 * numpy.random.normal(size=m)
y = numpy.concatenate([y1[:, None], y2[:, None]], axis=1)
missing = numpy.random.binomial(1, .2, (m, n)).astype(bool)
X_full = X.copy()
X[missing] = None
idx5 = (1 - missing[:, 5]).astype(bool)
idx6 = (1 - missing[:, 6]).astype(bool)
# Fit an Earth model
model = Earth(max_degree=5, minspan_alpha=.5, allow_missing=True,
enable_pruning=True, thresh=.001, smooth=True,
verbose=True)
model.fit(X, y)
# Print the model
print(model.trace())
print(model.summary())
# Plot the model
y_hat = model.predict(X)
fig = plt.figure()
for j in [0, 1]:
ax1 = fig.add_subplot(3, 4, 1 + 2*j)
ax1.plot(X_full[idx5, 5], y[idx5, j], 'b.')
ax1.plot(X_full[idx5, 5], y_hat[idx5, j], 'r.')
ax1.set_xlim(-40, 40)
ax1.set_title('x5 present')
ax1.set_xlabel('x5')
ax1.set_ylabel('sin' if j == 0 else 'cos')
ax2 = fig.add_subplot(3, 4, 2 + 2*j)
ax2.plot(X_full[idx6, 6], y[idx6, j], 'b.')
ax2.plot(X_full[idx6, 6], y_hat[idx6, j], 'r.')
ax2.set_xlim(-40, 40)
ax2.set_title('x6 present')
ax2.set_xlabel('x6')
ax2.set_ylabel('sin' if j == 0 else 'cos')
ax3 = fig.add_subplot(3, 4, 5 + 2*j, sharex=ax1)
ax3.plot(X_full[~idx6, 5], y[~idx6, j], 'b.')
ax3.plot(X_full[~idx6, 5], y_hat[~idx6, j], 'r.')
ax3.set_title('x6 missing')
ax3.set_xlabel('x5')
ax3.set_ylabel('sin' if j == 0 else 'cos')
ax4 = fig.add_subplot(3, 4, 6 + 2*j, sharex=ax2)
ax4.plot(X_full[~idx5, 6], y[~idx5, j], 'b.')
ax4.plot(X_full[~idx5, 6], y_hat[~idx5, j], 'r.')
ax4.set_title('x5 missing')
ax4.set_xlabel('x6')
ax4.set_ylabel('sin' if j == 0 else 'cos')
ax5 = fig.add_subplot(3, 4, 9 + 2*j, sharex=ax1)
ax5.plot(X_full[(~idx6) & (~idx5), 5], y[(~idx6) & (~idx5), j], 'b.')
ax5.plot(X_full[(~idx6) & (~idx5), 5], y_hat[(~idx6) & (~idx5), j], 'r.')
ax5.set_title('both missing')
ax5.set_xlabel('x5')
ax5.set_ylabel('sin' if j == 0 else 'cos')
ax6 = fig.add_subplot(3, 4, 10 + 2*j, sharex=ax2)
ax6.plot(X_full[(~idx6) & (~idx5), 6], y[(~idx6) & (~idx5), j], 'b.')
ax6.plot(X_full[(~idx6) & (~idx5), 6], y_hat[(~idx6) & (~idx5), j], 'r.')
ax6.set_title('both missing')
ax6.set_xlabel('x6')
ax6.set_ylabel('sin' if j == 0 else 'cos')
fig.tight_layout()
plt.show()
Total running time of the script: (0 minutes 59.852 seconds)
Download Python source code:
plot_multicolumn.py
Download IPython notebook:
plot_multicolumn.ipynb