Plotting sine function with redundant predictors an missing data¶
An example plotting a fit of the sine function. There are two redundant predictors, each of which has independent and random missingness.
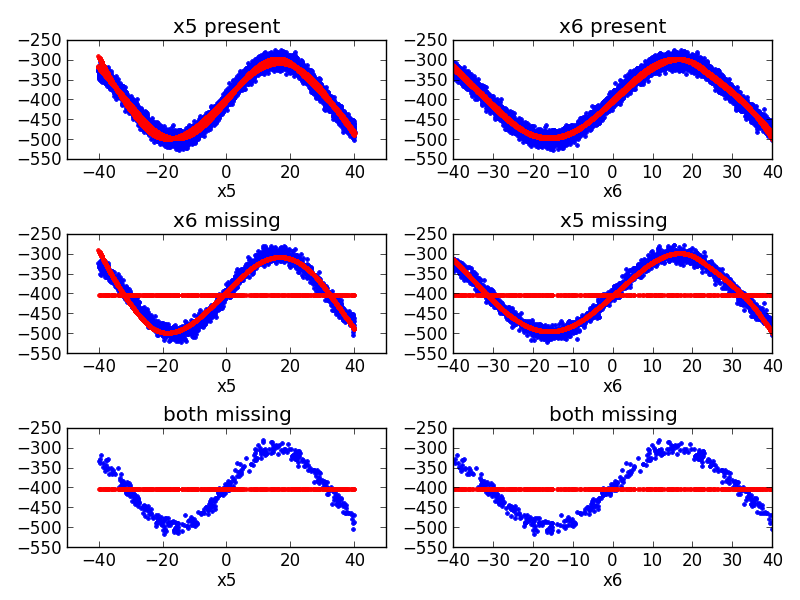
Out:
Beginning forward pass
---------------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
---------------------------------------------------------------------
0 - - - 4399.475105 1 4400.355 0.000 0.000
1 0 6 484 3218.482202 5 3225.575 0.268 0.267
2 3 6 7115 1000.371913 7 1003.581 0.773 0.772
3 0 5 1997 864.281682 11 868.794 0.804 0.803
4 10 5 584 587.091344 13 590.748 0.867 0.866
5 3 5 2524 366.234325 17 369.256 0.917 0.916
6 10 6 7684 282.087284 21 284.987 0.936 0.935
7 5 6 4061 278.832597 23 281.982 0.937 0.936
-------------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Beginning pruning pass
------------------------------------------------
iter bf terms mse gcv rsq grsq
------------------------------------------------
0 - 23 278.84 281.989 0.937 0.936
1 8 22 278.84 281.848 0.937 0.936
2 13 21 278.84 281.706 0.937 0.936
3 1 20 278.84 281.565 0.937 0.936
4 17 19 278.84 281.423 0.937 0.936
5 19 18 278.85 281.292 0.937 0.936
6 21 17 278.92 281.220 0.937 0.936
7 16 16 279.59 281.753 0.936 0.936
8 22 15 284.83 286.895 0.935 0.935
9 3 14 315.12 317.240 0.928 0.928
10 2 13 397.83 400.308 0.910 0.909
11 18 12 533.09 536.137 0.879 0.878
12 20 11 572.89 575.885 0.870 0.869
13 4 10 637.45 640.460 0.855 0.854
14 6 9 793.57 796.916 0.820 0.819
15 15 8 897.20 900.533 0.796 0.795
16 5 7 934.71 937.707 0.788 0.787
17 14 6 1017.38 1020.134 0.769 0.768
18 11 5 1258.44 1261.214 0.714 0.713
19 7 4 2635.44 2639.922 0.401 0.400
20 9 3 3192.33 3196.161 0.274 0.274
21 12 2 4039.23 4042.060 0.082 0.081
22 10 1 4399.48 4400.355 -0.000 -0.000
----------------------------------------------------
Selected iteration: 6
Earth Model
-----------------------------------------------------------------------------------------------------------------------------------------------
Basis Function Pruned Coefficient
-----------------------------------------------------------------------------------------------------------------------------------------------
(Intercept) No -477.431
present(x6) Yes None
missing(x6) No 72.659
C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No 1.7703
C(x6|s=-1,-32.2065,-24.4145,-7.42951)*present(x6) No 10.543
C(x6|s=+1,-7.42951,9.55548,21.7265)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No -0.232449
C(x6|s=-1,-7.42951,9.55548,21.7265)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No -0.35568
present(x5) No 113.492
missing(x5) Yes None
C(x5|s=+1,5.38057,22.2377,31.1865)*present(x5) No -11.1024
C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) No -2.39991
C(x5|s=+1,-25.8212,-11.4766,5.38057)*C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) No 0.222427
C(x5|s=-1,-25.8212,-11.4766,5.38057)*C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) No 0.260225
present(x5)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) Yes None
missing(x5)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No 4.96007
C(x5|s=+1,-15.4729,9.21999,24.6777)*present(x5)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No 0.210823
C(x5|s=-1,-15.4729,9.21999,24.6777)*present(x5)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No 0.00366201
present(x6)*C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) Yes None
missing(x6)*C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) No -5.024
C(x6|s=+1,-25.7228,-11.4472,14.2662)*present(x6)*C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) Yes None
C(x6|s=-1,-25.7228,-11.4472,14.2662)*present(x6)*C(x5|s=-1,5.38057,22.2377,31.1865)*present(x5) No -0.24299
C(x6|s=+1,21.7265,33.8976,36.9386)*C(x6|s=+1,-7.42951,9.55548,21.7265)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) Yes None
C(x6|s=-1,21.7265,33.8976,36.9386)*C(x6|s=+1,-7.42951,9.55548,21.7265)*C(x6|s=+1,-32.2065,-24.4145,-7.42951)*present(x6) No -0.00262933
-----------------------------------------------------------------------------------------------------------------------------------------------
MSE: 279.9548, GCV: 282.2646, RSQ: 0.9364, GRSQ: 0.9359
import numpy
import matplotlib.pyplot as plt
from pyearth import Earth
# Create some fake data
numpy.random.seed(2)
m = 10000
n = 10
X = 80 * numpy.random.uniform(size=(m, n)) - 40
X[:, 5] = X[:, 6] + numpy.random.normal(0, .1, m)
y = 100 * \
(numpy.sin((X[:, 5] + X[:, 6]) / 20) - 4.0) + \
10 * numpy.random.normal(size=m)
missing = numpy.random.binomial(1, .2, (m, n)).astype(bool)
X_full = X.copy()
X[missing] = None
idx5 = (1 - missing[:, 5]).astype(bool)
idx6 = (1 - missing[:, 6]).astype(bool)
# Fit an Earth model
model = Earth(max_degree=5, minspan_alpha=.5, allow_missing=True,
enable_pruning=True, thresh=.001, smooth=True, verbose=2)
model.fit(X, y)
# Print the model
print(model.summary())
# Plot the model
y_hat = model.predict(X)
fig = plt.figure()
ax1 = fig.add_subplot(3, 2, 1)
ax1.plot(X_full[idx5, 5], y[idx5], 'b.')
ax1.plot(X_full[idx5, 5], y_hat[idx5], 'r.')
ax1.set_xlim(-40, 40)
ax1.set_title('x5 present')
ax1.set_xlabel('x5')
ax2 = fig.add_subplot(3, 2, 2)
ax2.plot(X_full[idx6, 6], y[idx6], 'b.')
ax2.plot(X_full[idx6, 6], y_hat[idx6], 'r.')
ax2.set_xlim(-40, 40)
ax2.set_title('x6 present')
ax2.set_xlabel('x6')
ax3 = fig.add_subplot(3, 2, 3, sharex=ax1)
ax3.plot(X_full[~idx6, 5], y[~idx6], 'b.')
ax3.plot(X_full[~idx6, 5], y_hat[~idx6], 'r.')
ax3.set_title('x6 missing')
ax3.set_xlabel('x5')
ax4 = fig.add_subplot(3, 2, 4, sharex=ax2)
ax4.plot(X_full[~idx5, 6], y[~idx5], 'b.')
ax4.plot(X_full[~idx5, 6], y_hat[~idx5], 'r.')
ax4.set_title('x5 missing')
ax4.set_xlabel('x6')
ax5 = fig.add_subplot(3, 2, 5, sharex=ax1)
ax5.plot(X_full[(~idx6) & (~idx5), 5], y[(~idx6) & (~idx5)], 'b.')
ax5.plot(X_full[(~idx6) & (~idx5), 5], y_hat[(~idx6) & (~idx5)], 'r.')
ax5.set_title('both missing')
ax5.set_xlabel('x5')
ax6 = fig.add_subplot(3, 2, 6, sharex=ax2)
ax6.plot(X_full[(~idx6) & (~idx5), 6], y[(~idx6) & (~idx5)], 'b.')
ax6.plot(X_full[(~idx6) & (~idx5), 6], y_hat[(~idx6) & (~idx5)], 'r.')
ax6.set_title('both missing')
ax6.set_xlabel('x6')
fig.tight_layout()
plt.show()
Total running time of the script: (0 minutes 10.316 seconds)
Download Python source code:
plot_missing_data_problem.py
Download IPython notebook:
plot_missing_data_problem.ipynb