Introduction¶
The py-earth package is a Python implementation of Jerome Friedman’s Multivariate Adaptive Regression Splines algorithm, in the style of scikit-learn. For more information about Multivariate Adaptive Regression Splines, see below. Py-earth is written in Python and Cython. It provides an interface that is compatible with scikit-learn’s Estimator, Predictor, Transformer, and Model interfaces. Py-earth accommodates input in the form of numpy arrays, pandas DataFrames, patsy DesignMatrix objects, or most anything that can be converted into an arrray of floats. Fitted models can be pickled for later use.
Multivariate Adaptive Regression Splines¶
Multivariate adaptive regression splines, implemented by the Earth class, is a flexible regression method that automatically searches for interactions and non-linear relationships. Earth models can be thought of as linear models in a higher dimensional basis space. Each term in an Earth model is a product of so called “hinge functions”. A hinge function is a function that’s equal to its argument where that argument is greater than zero and is zero everywhere else.
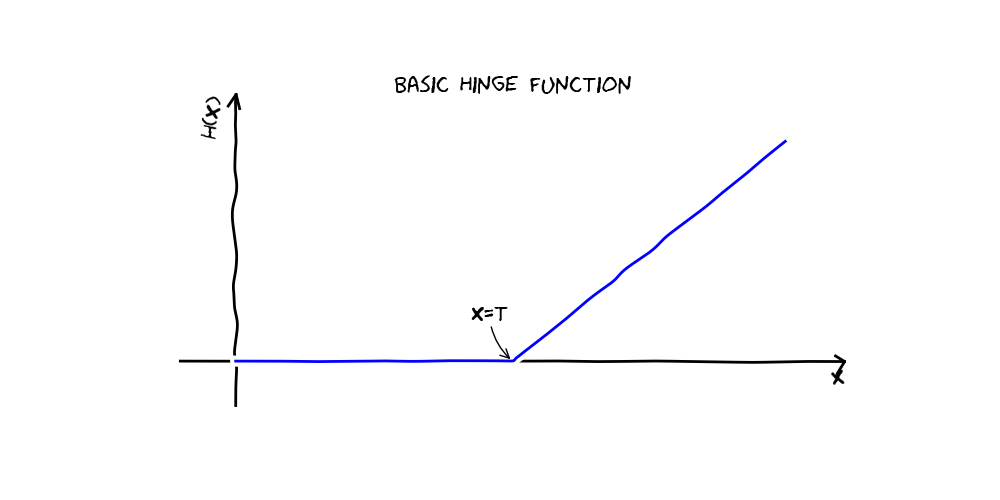
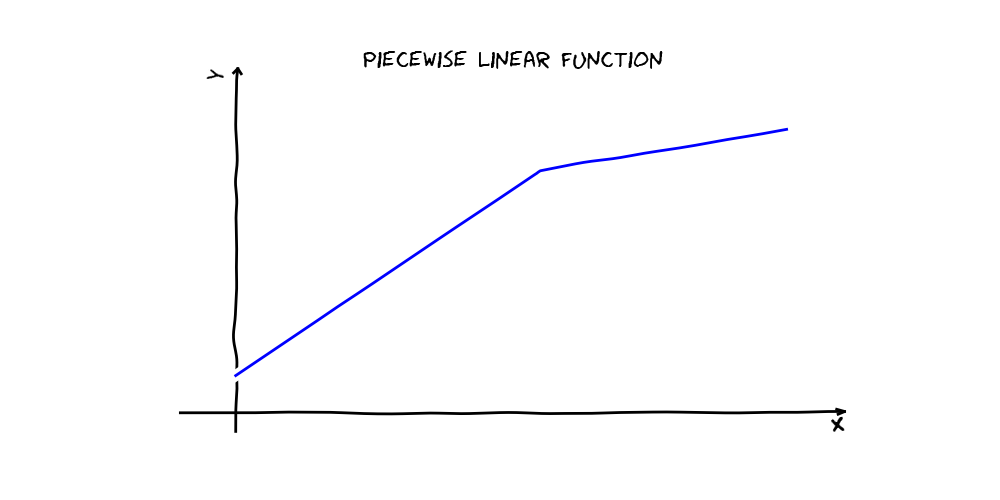
An Earth model is a linear combination of basis functions, each of which is a product of one or more of the following:
- A constant
- Linear functions of input variables
- Hinge functions of input variables
For example, a simple piecewise linear function in one variable can be expressed as a linear combination of two hinge functions and a constant (see below). During fitting, the Earth class automatically determines which variables and basis functions to use. The algorithm has two stages. First, the forward pass searches for terms that locally minimize squared error loss on the training set. Next, a pruning pass selects a subset of those terms that produces a locally minimal generalized cross-validation (GCV) score. The GCV score is not actually based on cross-validation, but rather is meant to approximate a true cross-validation score by penalizing model complexity. The final result is a set of basis functions that is nonlinear in the original feature space, may include interactions, and is likely to generalize well.
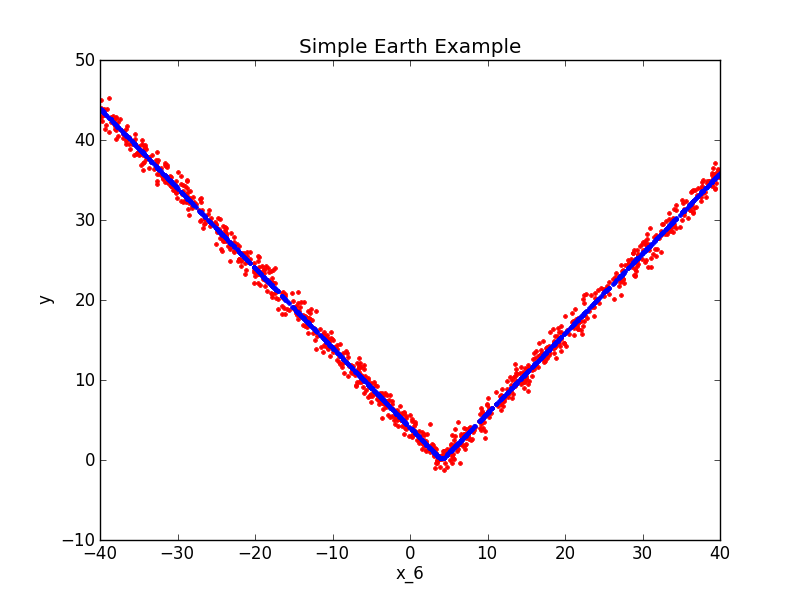
A Simple Earth Example¶
import numpy
from pyearth import Earth
from matplotlib import pyplot
#Create some fake data
numpy.random.seed(0)
m = 1000
n = 10
X = 80*numpy.random.uniform(size=(m,n)) - 40
y = numpy.abs(X[:,6] - 4.0) + 1*numpy.random.normal(size=m)
#Fit an Earth model
model = Earth()
model.fit(X,y)
#Print the model
print(model.trace())
print(model.summary())
#Plot the model
y_hat = model.predict(X)
pyplot.figure()
pyplot.plot(X[:,6],y,'r.')
pyplot.plot(X[:,6],y_hat,'b.')
pyplot.xlabel('x_6')
pyplot.ylabel('y')
pyplot.title('Simple Earth Example')
pyplot.show()
Bibliography¶
| [Bjo96] | Ake Bjorck. Numerical Methods for Least Squares Problems. Society for Industrial and Applied Mathematics, Philadelphia, 1996. ISBN 0898713609. |
| [Fri93] | (1, 2) Jerome H. Friedman. Technical Report No. 110: Fast MARS. Technical Report, Stanford University Department of Statistics, 1993. URL: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:Fast+MARS#0. |
| [Fri91a] | (1, 2) JH Friedman. Multivariate adaptive regression splines. The annals of statistics, 19(1):1–67, 1991. URL: http://www.jstor.org/stable/10.2307/2241837. |
| [Fri91b] | (1, 2) JH Friedman. Technical Report No. 108: Estimating functions of mixed ordinal and categorical variables using adaptive splines. Technical Report, Stanford University Department of Statistics, 1991. URL: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:Estimating+functions+of+mixed+ordinal+and+categorical+variables+using+adaptive+splines#0. |
| [GVanLoan96] | Gene Golub and Charles Van Loan. Matrix Computations. Johns Hopkins University Press, 3 edition, 1996. |
| [HTF09] | Trevor Hastie, Robert Tibshirani, and Jerome Friedman. Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Science+Business Media, New York, 2 edition, 2009. |
| [Mil12] | (1, 2) Stephen Millborrow. earth: Multivariate Adaptive Regression Spline Models. 2012. URL: http://cran.r-project.org/web/packages/earth/index.html. |
| [Ste98] | G. W. Stewart. Matrix Algorithms Volume 1: Basic Decompositions. Society for Industrial and Applied Mathematics, Philadelphia, 1998. ISBN 0898714141. |
References [HTF09], [Mil12], [Fri91a], [Fri93], and [Fri91b] contain discussions likely to be useful to users of py-earth. References [Fri91a], [Mil12], [Bjo96], [Ste98], [GVanLoan96], [Fri93], and [Fri91b] were useful during the implementation process.
API¶
-
class
pyearth.Earth(max_terms=None, max_degree=None, allow_missing=False, penalty=None, endspan_alpha=None, endspan=None, minspan_alpha=None, minspan=None, thresh=None, zero_tol=None, min_search_points=None, check_every=None, allow_linear=None, use_fast=None, fast_K=None, fast_h=None, smooth=None, enable_pruning=True, feature_importance_type=None, verbose=0)[source]¶ Multivariate Adaptive Regression Splines
A flexible regression method that automatically searches for interactions and non-linear relationships. Earth models can be thought of as linear models in a higher dimensional basis space (specifically, a multivariate truncated power spline basis). Each term in an Earth model is a product of so called “hinge functions”. A hinge function is a function that’s equal to its argument where that argument is greater than zero and is zero everywhere else.
The multivariate adaptive regression splines algorithm has two stages. First, the forward pass searches for terms in the truncated power spline basis that locally minimize the squared error loss of the training set. Next, a pruning pass selects a subset of those terms that produces a locally minimal generalized cross-validation (GCV) score. The GCV score is not actually based on cross-validation, but rather is meant to approximate a true cross-validation score by penalizing model complexity. The final result is a set of terms that is nonlinear in the original feature space, may include interactions, and is likely to generalize well.
The Earth class supports dense input only. Data structures from the pandas and patsy modules are supported, but are copied into numpy arrays for computation. No copy is made if the inputs are numpy float64 arrays. Earth objects can be serialized using the pickle module and copied using the copy module.
Parameters: max_terms : int, optional (default=min(2 * n + m // 10, 400)),
where n is the number of features and m is the number of rows)
The maximum number of terms generated by the forward pass. All memory is allocated at the beginning of the forward pass, so setting max_terms to a very high number on a system with insufficient memory may cause a MemoryError at the start of the forward pass.
max_degree : int, optional (default=1)
The maximum degree of terms generated by the forward pass.
allow_missing : boolean, optional (default=False)
If True, use missing data method described in [3]. Use missing argument to determine missingness or,if X is a pandas DataFrame, infer missingness from X.
penalty : float, optional (default=3.0)
A smoothing parameter used to calculate GCV and GRSQ. Used during the pruning pass and to determine whether to add a hinge or linear basis function during the forward pass. See the d parameter in equation 32, Friedman, 1991.
endspan_alpha : float, optional, probability between 0 and 1 (default=0.05)
A parameter controlling the calculation of the endspan parameter (below). The endspan parameter is calculated as round(3 - log2(endspan_alpha/n)), where n is the number of features. The endspan_alpha parameter represents the probability of a run of positive or negative error values on either end of the data vector of any feature in the data set. See equation 45, Friedman, 1991.
endspan : int, optional (default=-1)
The number of extreme data values of each feature not eligible as knot locations. If endspan is set to -1 (default) then the endspan parameter is calculated based on endspan_alpah (above). If endspan is set to a positive integer then endspan_alpha is ignored.
minspan_alpha : float, optional, probability between 0 and 1 (default=0.05)
A parameter controlling the calculation of the minspan parameter (below). The minspan parameter is calculated as
(int) -log2(-(1.0/(n*count))*log(1.0-minspan_alpha)) / 2.5
where n is the number of features and count is the number of points at which the parent term is non-zero. The minspan_alpha parameter represents the probability of a run of positive or negative error values between adjacent knots separated by minspan intervening data points. See equation 43, Friedman, 1991.
minspan : int, optional (default=-1)
The minimal number of data points between knots. If minspan is set to -1 (default) then the minspan parameter is calculated based on minspan_alpha (above). If minspan is set to a positive integer then minspan_alpha is ignored.
thresh : float, optional (default=0.001)
Parameter used when evaluating stopping conditions for the forward pass. If either RSQ > 1 - thresh or if RSQ increases by less than thresh for a forward pass iteration then the forward pass is terminated.
zero_tol : float, optional (default=1e-12)
Used when determining whether a floating point number is zero during the forward pass. This is important in determining linear dependence and in the fast update procedure. There should normally be no reason to change zero_tol from its default. However, if nans are showing up during the forward pass or the forward pass seems to be terminating unexpectedly, consider adjusting zero_tol.
min_search_points : int, optional (default=100)
Used to calculate check_every (below). The minimum samples necessary for check_every to be greater than 1. The check_every parameter is calculated as
(int) m / min_search_points
if m > min_search_points, where m is the number of samples in the training set. If m <= min_search_points then check_every is set to 1.
check_every : int, optional (default=-1)
If check_every > 0, only one of every check_every sorted data points is considered as a candidate knot. If check_every is set to -1 then the check_every parameter is calculated based on min_search_points (above).
allow_linear : bool, optional (default=True)
If True, the forward pass will check the GCV of each new pair of terms and, if it’s not an improvement on a single term with no knot (called a linear term, although it may actually be a product of a linear term with some other parent term), then only that single, knotless term will be used. If False, that behavior is disabled and all terms will have knots except those with variables specified by the linvars argument (see the fit method).
use_fast : bool, optional (default=False)
if True, use the approximation procedure defined in [2] to speed up the forward pass. The procedure uses two hyper-parameters : fast_K and fast_h. Check below for more details.
fast_K : int, optional (default=5)
Only used if use_fast is True. As defined in [2], section 3.0, it defines the maximum number of basis functions to look at when we search for a parent, that is we look at only the fast_K top terms ranked by the mean squared error of the model the last time the term was chosen as a parent. The smaller fast_K is, the more gains in speed we get but the more approximate is the result. If fast_K is the maximum number of terms and fast_h is 1, the behavior is the same as in the normal case (when use_fast is False).
fast_h : int, optional (default=1)
Only used if use_fast is True. As defined in [2], section 4.0, it determines the number of iterations before repassing through all the variables when searching for the variable to use for a given parent term. Before reaching fast_h number of iterations only the last chosen variable for the parent term is used. The bigger fast_h is, the more speed gains we get, but the result is more approximate.
smooth : bool, optional (default=False)
If True, the model will be smoothed such that it has continuous first derivatives. For details, see section 3.7, Friedman, 1991.
enable_pruning : bool, optional(default=True)
If False, the pruning pass will be skipped.
feature_importance_type: string or list of strings, optional (default=None)
Specify which kind of feature importance criteria to compute. Currently three criteria are supported : ‘gcv’, ‘rss’ and ‘nb_subsets’. By default (when it is None), no feature importance is computed. Feature importance is a measure of the effect of the features on the outputs. For each feature, the values go from 0 to 1 and sum up to 1. A high value means the feature have in average (over the population) a large effect on the outputs. See [4], section 12.3 for more information about the criteria.
verbose : int, optional(default=0)
If verbose >= 1, print out progress information during fitting. If verbose >= 2, also print out information on numerical difficulties if encountered during fitting. If verbose >= 3, print even more information that is probably only useful to the developers of py-earth.
References
[R1] Friedman, Jerome. Multivariate Adaptive Regression Splines. Annals of Statistics. Volume 19, Number 1 (1991), 1-67. [R2] Fast MARS, Jerome H.Friedman, Technical Report No.110, May 1993. [R3] Estimating Functions of Mixed Ordinal and Categorical Variables Using Adaptive Splines, Jerome H.Friedman, Technical Report No.108, June 1991. [R4] http://www.milbo.org/doc/earth-notes.pdf Attributes
coef_ (array, shape = [pruned basis length, number of outputs]) The weights of the model terms that have not been pruned. basis_ (_basis.Basis) An object representing model terms. Each term is a product of constant, linear, and hinge functions of the input features. mse_ (float) The mean squared error of the model after the final linear fit. If sample_weight and/or output_weight are given, this score is weighted appropriately. rsq_ (float) The generalized r^2 of the model after the final linear fit. If sample_weight and/or output_weight are given, this score is weighted appropriately. gcv_ (float) The generalized cross validation (GCV) score of the model after the final linear fit. If sample_weight and/or output_weight are given, this score is weighted appropriately. grsq_ (float) An r^2 like score based on the GCV. If sample_weight and/or output_weight are given, this score is weighted appropriately. forward_pass_record_ (_record.ForwardPassRecord) An object containing information about the forward pass, such as training loss function values after each iteration and the final stopping condition. pruning_pass_record_ (_record.PruningPassRecord) An object containing information about the pruning pass, such as training loss function values after each iteration and the selected optimal iteration. xlabels_ (list) List of column names for training predictors. Defaults to [‘x0’,’x1’,....] if column names are not provided. allow_missing_ (list) List of booleans indicating whether each variable is allowed to be missing. Set during training. A variable may be missing only if fitting included missing data for that variable. feature_importances_: array of shape [m] or dict m is the number of features. if one feature importance type is specified, it is an array of shape m. If several feature importance types are specified, then it is dict where each key is a feature importance type name and its corresponding value is an array of shape m. -
fit(X, y=None, sample_weight=None, output_weight=None, missing=None, xlabels=None, linvars=[])[source]¶ Fit an Earth model to the input data X and y.
Parameters: X : array-like, shape = [m, n] where m is the number of samples
and n is the number of features the training predictors. The X parameter can be a numpy array, a pandas DataFrame, a patsy DesignMatrix, or a tuple of patsy DesignMatrix objects as output by patsy.dmatrices.
y : array-like, optional (default=None), shape = [m, p] where m is the
number of samples The training response, p the number of outputs. The y parameter can be a numpy array, a pandas DataFrame, a Patsy DesignMatrix, or can be left as None (default) if X was the output of a call to patsy.dmatrices (in which case, X contains the response).
sample_weight : array-like, optional (default=None), shape = [m]
where m is the number of samples. Sample weights for training. Weights must be greater than or equal to zero. Rows with zero weight do not contribute at all. Weights are useful when dealing with heteroscedasticity. In such cases, the weight should be proportional to the inverse of the (known) variance.
output_weight : array-like, optional (default=None), shape = [p]
where p is the number of outputs. Output weights for training. Weights must be greater than or equal to zero. Output with zero weight do not contribute at all.
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
linvars : iterable of strings or ints, optional (empty by default)
Used to specify features that may only enter terms as linear basis functions (without knots). Can include both column numbers and column names (see xlabels, below). If left empty, some variables may still enter linearly during the forward pass if no knot would provide a reduction in GCV compared to the linear function. Note that this feature differs from the R package earth.
xlabels : iterable of strings, optional (empty by default)
The xlabels argument can be used to assign names to data columns. This argument is not generally needed, as names can be captured automatically from most standard data structures. If included, must have length n, where n is the number of features. Note that column order is used to compute term values and make predictions, not column names.
-
fit_transform(X, y=None, **fit_params)¶ Fit to data, then transform it.
Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.
Parameters: X : numpy array of shape [n_samples, n_features]
Training set.
y : numpy array of shape [n_samples]
Target values.
Returns: X_new : numpy array of shape [n_samples, n_features_new]
Transformed array.
-
forward_pass(X, y=None, sample_weight=None, output_weight=None, missing=None, xlabels=None, linvars=[], skip_scrub=False)[source]¶ Perform the forward pass of the multivariate adaptive regression splines algorithm. Users will normally want to call the fit method instead, which performs the forward pass, the pruning pass, and a linear fit to determine the final model coefficients.
Parameters: X : array-like, shape = [m, n] where m is the number of samples and n
is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, a patsy DesignMatrix, or a tuple of patsy DesignMatrix objects as output by patsy.dmatrices.
y : array-like, optional (default=None), shape = [m, p] where m is the
number of samples, p the number of outputs. The y parameter can be a numpy array, a pandas DataFrame, a Patsy DesignMatrix, or can be left as None (default) if X was the output of a call to patsy.dmatrices (in which case, X contains the response).
sample_weight : array-like, optional (default=None), shape = [m]
where m is the number of samples. Sample weights for training. Weights must be greater than or equal to zero. Rows with zero weight do not contribute at all. Weights are useful when dealing with heteroscedasticity. In such cases, the weight should be proportional to the inverse of the (known) variance.
output_weight : array-like, optional (default=None), shape = [p]
where p is the number of outputs. The total mean squared error (MSE) is a weighted sum of mean squared errors (MSE) associated to each output, where the weights are given by output_weight. Output weights must be greater than or equal to zero. Outputs with zero weight do not contribute at all to the total mean squared error (MSE).
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
linvars : iterable of strings or ints, optional (empty by default)
Used to specify features that may only enter terms as linear basis functions (without knots). Can include both column numbers and column names (see xlabels, below).
xlabels : iterable of strings, optional (empty by default)
The xlabels argument can be used to assign names to data columns. This argument is not generally needed, as names can be captured automatically from most standard data structures. If included, must have length n, where n is the number of features. Note that column order is used to compute term values and make predictions, not column names.
-
get_params(deep=True)¶ Get parameters for this estimator.
Parameters: deep: boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
-
linear_fit(X, y=None, sample_weight=None, output_weight=None, missing=None, skip_scrub=False)[source]¶ Solve the linear least squares problem to determine the coefficients of the unpruned basis functions.
Parameters: X : array-like, shape = [m, n] where m is the number of samples and n
is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, a patsy DesignMatrix, or a tuple of patsy DesignMatrix objects as output by patsy.dmatrices.
y : array-like, optional (default=None), shape = [m, p] where m is the
number of samples, p the number of outputs. The y parameter can be a numpy array, a pandas DataFrame, a Patsy DesignMatrix, or can be left as None (default) if X was the output of a call to patsy.dmatrices (in which case, X contains the response).
sample_weight : array-like, optional (default=None), shape = [m]
where m is the number of samples. Sample weights for training. Weights must be greater than or equal to zero. Rows with zero weight do not contribute at all. Weights are useful when dealing with heteroscedasticity. In such cases, the weight should be proportional to the inverse of the (known) variance.
output_weight : array-like, optional (default=None), shape = [p]
where p is the number of outputs. The total mean squared error (MSE) is a weighted sum of mean squared errors (MSE) associated to each output, where the weights are given by output_weight. Output weights must be greater than or equal to zero. Outputs with zero weight do not contribute at all to the total mean squared error (MSE).
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
-
predict(X, missing=None, skip_scrub=False)[source]¶ - Predict the response based on the input data X.
Parameters: X : array-like, shape = [m, n] where m is the number of samples and n
is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix.
- missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
Returns: y : array of shape = [m] or [m, p] where m is the number of samples
and p is the number of outputs The predicted values.
-
predict_deriv(X, variables=None, missing=None)[source]¶ - Predict the first derivatives of the response based on the input data X.
Parameters: X : array-like, shape = [m, n] where m is the number of samples and n
is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix.
- missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
- variables : list
The variables over which derivatives will be computed. Each column in the resulting array corresponds to a variable. If not specified, all variables are used (even if some are not relevant to the final model and have derivatives that are identically zero).
Returns: X_deriv : array of shape = [m, n, p] where m is the number of samples, n
is the number of features if ‘variables’ is not specified otherwise it is len(variables) and p is the number of outputs. For each sample, X_deriv represents the first derivative of each response with respect to each variable.
-
pruning_pass(X, y=None, sample_weight=None, output_weight=None, missing=None, skip_scrub=False)[source]¶ Perform the pruning pass of the multivariate adaptive regression splines algorithm. Users will normally want to call the fit method instead, which performs the forward pass, the pruning pass, and a linear fit to determine the final model coefficients.
Parameters: X : array-like, shape = [m, n] where m is the number of samples
and n is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, a patsy DesignMatrix, or a tuple of patsy DesignMatrix objects as output by patsy.dmatrices.
y : array-like, optional (default=None), shape = [m, p] where m is the
number of samples, p the number of outputs. The y parameter can be a numpy array, a pandas DataFrame, a Patsy DesignMatrix, or can be left as None (default) if X was the output of a call to patsy.dmatrices (in which case, X contains the response).
sample_weight : array-like, optional (default=None), shape = [m]
where m is the number of samples. Sample weights for training. Weights must be greater than or equal to zero. Rows with zero weight do not contribute at all. Weights are useful when dealing with heteroscedasticity. In such cases, the weight should be proportional to the inverse of the (known) variance.
output_weight : array-like, optional (default=None), shape = [p]
where p is the number of outputs. The total mean squared error (MSE) is a weighted sum of mean squared errors (MSE) associated to each output, where the weights are given by output_weight. Output weights must be greater than or equal to zero. Outputs with zero weight do not contribute at all to the total mean squared error (MSE).
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
-
score(X, y=None, sample_weight=None, output_weight=None, missing=None, skip_scrub=False)[source]¶ Calculate the generalized r^2 of the model on data X and y.
Parameters: X : array-like, shape = [m, n] where m is the number of samples
and n is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, a patsy DesignMatrix, or a tuple of patsy DesignMatrix objects as output by patsy.dmatrices.
y : array-like, optional (default=None), shape = [m, p] where m is the
number of samples, p the number of outputs. The y parameter can be a numpy array, a pandas DataFrame, a Patsy DesignMatrix, or can be left as None (default) if X was the output of a call to patsy.dmatrices (in which case, X contains the response).
sample_weight : array-like, optional (default=None), shape = [m]
where m is the number of samples. Sample weights for training. Weights must be greater than or equal to zero. Rows with zero weight do not contribute at all. Weights are useful when dealing with heteroscedasticity. In such cases, the weight should be proportional to the inverse of the (known) variance.
output_weight : array-like, optional (default=None), shape = [p]
where p is the number of outputs. The total mean squared error (MSE) is a weighted sum of mean squared errors (MSE) associated to each output, where the weights are given by output_weight. Output weights must be greater than or equal to zero. Outputs with zero weight do not contribute at all to the total mean squared error (MSE).
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
Returns: score : float with a maximum value of 1 (it can be negative). The score
is the generalized r^2 of the model on data X and y, the higher the score the better the fit is.
-
score_samples(X, y=None, missing=None)[source]¶ Calculate sample-wise fit scores.
Parameters: X : array-like, shape = [m, n] where m is the number of samples
and n is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, a patsy DesignMatrix, or a tuple of patsy DesignMatrix objects as output by patsy.dmatrices.
y : array-like, optional (default=None), shape = [m, p] where m is the
number of samples, p the number of outputs. The y parameter can be a numpy array, a pandas DataFrame, a Patsy DesignMatrix, or can be left as None (default) if X was the output of a call to patsy.dmatrices (in which case, X contains the response).
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
Returns: scores : array of shape=[m, p] of floats with maximum value of 1
(it can be negative). The scores represent how good each output of each example is predicted, a perfect score would be 1 (the score can be negative).
-
set_params(**params)¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: self
-
summary_feature_importances(sort_by=None)[source]¶ Returns a string containing a printable summary of the estimated feature importances.
Parameters: sory_by : string, optional
it refers to a feature importance type name : ‘gcv’, ‘rss’ or ‘nb_subsets’. In case it is provided, the features are sorted according to the feature importance type corresponding to sort_by. In case it is not provided, the features are not sorted.
-
transform(X, missing=None)[source]¶ Transform X into the basis space. Normally, users will call the predict method instead, which both transforms into basis space calculates the weighted sum of basis terms to produce a prediction of the response. Users may wish to call transform directly in some cases. For example, users may wish to apply other statistical or machine learning algorithms, such as generalized linear regression, in basis space.
Parameters: X : array-like, shape = [m, n] where m is the number of samples and n
is the number of features The training predictors. The X parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix.
missing : array-like, shape = [m, n] where m is the number of samples
and n is the number of features. The missing parameter can be a numpy array, a pandas DataFrame, or a patsy DesignMatrix. All entries will be interpreted as boolean values, with True indicating the corresponding entry in X should be interpreted as missing. If the missing argument not used but the X argument is a pandas DataFrame, missing will be inferred from X if allow_missing is True.
Returns: B: array of shape [m, nb_terms] where m is the number of samples and
nb_terms is the number of terms (or basis functions) obtained after fitting (which is the number of elements of the attribute basis_). B represents the values of the basis functions evaluated at each sample.
-