Plotting simple sine function¶
A simple example plotting a fit of the sine function.
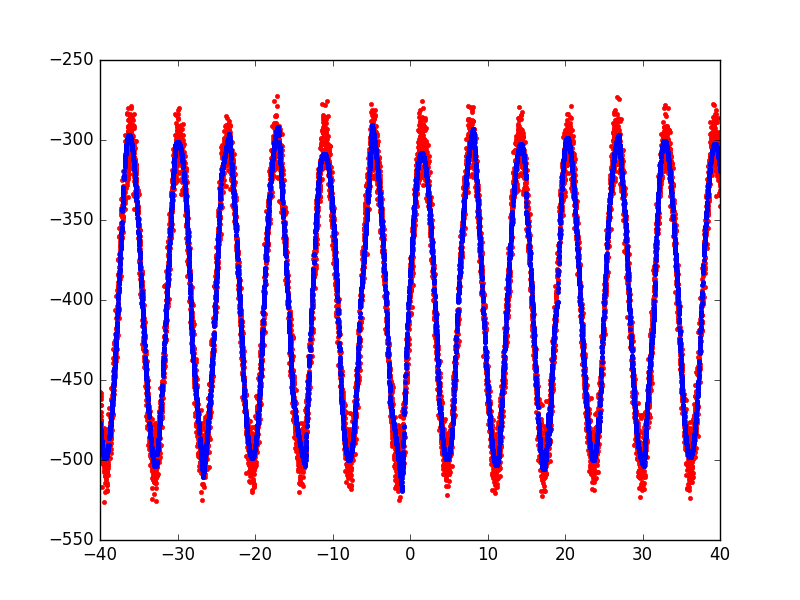
Out:
Beginning forward pass
---------------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
---------------------------------------------------------------------
0 - - - 5244.476631 1 5245.526 0.000 0.000
1 0 6 9961 5067.564966 3 5073.652 0.034 0.033
2 2 6 3206 4861.646322 5 4872.360 0.073 0.071
3 4 6 7844 4639.910399 7 4654.794 0.115 0.113
4 0 6 7260 4468.624616 9 4487.452 0.148 0.145
5 7 6 8157 4244.467266 11 4266.625 0.191 0.187
6 9 6 2242 3900.087914 13 3924.381 0.256 0.252
7 10 6 5832 3770.802883 15 3798.100 0.281 0.276
8 7 6 1644 3534.771940 17 3563.936 0.326 0.321
9 15 6 3475 3314.407980 19 3345.112 0.368 0.362
10 15 6 2648 3162.265769 21 3194.769 0.397 0.391
11 9 6 1923 3028.741358 23 3062.950 0.422 0.416
12 7 6 3624 2880.064377 25 2915.525 0.451 0.444
13 23 6 3486 2702.824122 27 2738.858 0.485 0.478
14 23 6 116 2545.534016 29 2582.069 0.515 0.508
15 4 6 8773 2422.575970 31 2459.823 0.538 0.531
16 2 6 803 2262.126670 33 2299.223 0.569 0.562
17 32 6 5864 2122.594794 35 2159.580 0.595 0.588
18 4 6 7610 1836.777669 37 1870.669 0.650 0.643
19 0 6 2035 1641.898343 39 1673.883 0.687 0.681
20 38 6 7332 1428.554810 41 1457.855 0.728 0.722
21 40 6 9013 1053.447265 43 1076.141 0.799 0.795
22 37 6 1206 758.322249 45 775.442 0.855 0.852
23 7 6 593 636.565160 47 651.594 0.879 0.876
24 43 6 6001 532.755707 49 545.886 0.898 0.896
25 23 6 1488 451.992938 51 463.602 0.914 0.912
26 37 6 6122 385.157239 53 395.450 0.927 0.925
27 7 6 6946 335.936149 55 345.263 0.936 0.934
28 32 6 3381 287.101417 57 295.372 0.945 0.944
29 24 6 1440 235.668475 59 242.704 0.955 0.954
30 32 6 8375 209.747432 61 216.228 0.960 0.959
31 45 6 500 196.500438 63 202.778 0.963 0.961
32 2 6 3553 184.151662 65 190.228 0.965 0.964
33 39 6 9809 173.669012 67 179.582 0.967 0.966
34 52 6 1334 161.396838 69 167.061 0.969 0.968
35 9 6 1940 154.513111 71 160.099 0.971 0.969
36 7 6 9087 147.735445 73 153.232 0.972 0.971
37 53 6 3475 141.226286 75 146.630 0.973 0.972
38 40 6 1097 135.344070 77 140.666 0.974 0.973
39 40 6 7450 129.288718 79 134.510 0.975 0.974
40 64 6 1948 124.662704 81 129.829 0.976 0.975
-------------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Beginning pruning pass
------------------------------------------------
iter bf terms mse gcv rsq grsq
------------------------------------------------
0 - 81 124.94 130.113 0.976 0.975
1 43 80 124.94 130.047 0.976 0.975
2 31 79 124.94 129.981 0.976 0.975
3 35 78 124.94 129.915 0.976 0.975
4 1 77 124.94 129.848 0.976 0.975
5 58 76 124.94 129.782 0.976 0.975
6 17 75 124.94 129.716 0.976 0.975
7 40 74 124.94 129.650 0.976 0.975
8 63 73 124.94 129.584 0.976 0.975
9 69 72 124.94 129.518 0.976 0.975
10 42 71 124.94 129.452 0.976 0.975
11 46 70 124.94 129.386 0.976 0.975
12 26 69 124.94 129.320 0.976 0.975
13 23 68 124.94 129.255 0.976 0.975
14 71 67 124.94 129.189 0.976 0.975
15 55 66 124.94 129.123 0.976 0.975
16 15 65 124.94 129.058 0.976 0.975
17 60 64 124.94 128.992 0.976 0.975
18 54 63 124.94 128.927 0.976 0.975
19 9 62 124.94 128.861 0.976 0.975
20 6 61 124.94 128.796 0.976 0.975
21 10 60 124.93 128.723 0.976 0.975
22 13 59 124.93 128.662 0.976 0.975
23 8 58 124.94 128.604 0.976 0.975
24 16 57 124.99 128.586 0.976 0.975
25 4 56 125.10 128.642 0.976 0.975
26 32 55 125.61 129.095 0.976 0.975
27 33 54 127.52 130.994 0.976 0.975
28 74 53 128.99 132.437 0.975 0.975
29 80 52 131.21 134.645 0.975 0.974
30 22 51 132.74 136.150 0.975 0.974
31 21 50 133.34 136.691 0.975 0.974
32 75 49 133.99 137.295 0.974 0.974
33 36 48 138.74 142.089 0.974 0.973
34 79 47 144.86 148.276 0.972 0.972
35 72 46 151.28 154.769 0.971 0.970
36 70 45 160.51 164.129 0.969 0.969
37 66 44 170.02 173.767 0.968 0.967
38 65 43 178.52 182.365 0.966 0.965
39 25 42 188.91 192.887 0.964 0.963
40 68 41 199.78 203.874 0.962 0.961
41 7 40 211.71 215.947 0.960 0.959
42 59 39 223.54 227.893 0.957 0.957
43 45 38 240.03 244.579 0.954 0.953
44 76 37 252.64 257.300 0.952 0.951
45 67 36 277.68 282.664 0.947 0.946
46 5 35 307.60 312.958 0.941 0.940
47 62 34 339.68 345.429 0.935 0.934
48 61 33 349.66 355.399 0.933 0.932
49 56 32 406.73 413.191 0.922 0.921
50 53 31 476.86 484.187 0.909 0.908
51 73 30 531.86 539.769 0.899 0.897
52 19 29 565.68 573.801 0.892 0.891
53 3 28 724.42 734.443 0.862 0.860
54 20 27 974.98 987.983 0.814 0.812
55 57 26 1241.03 1256.947 0.763 0.760
56 18 25 1547.42 1566.472 0.705 0.701
57 14 24 1934.24 1957.075 0.631 0.627
58 44 23 2135.76 2159.880 0.593 0.588
59 38 22 2283.01 2307.631 0.565 0.560
60 49 21 2339.81 2363.860 0.554 0.549
61 27 20 2504.83 2529.307 0.522 0.518
62 12 19 2702.93 2727.972 0.485 0.480
63 24 18 2955.40 2981.280 0.436 0.432
64 50 17 3260.70 3287.600 0.378 0.373
65 28 16 3372.40 3398.523 0.357 0.352
66 41 15 3598.03 3624.073 0.314 0.309
67 51 14 3906.02 3932.321 0.255 0.250
68 37 13 3982.16 4006.966 0.241 0.236
69 2 12 4090.99 4114.409 0.220 0.216
70 78 11 4427.86 4450.979 0.156 0.151
71 47 10 4472.96 4494.060 0.147 0.143
72 77 9 4524.47 4543.529 0.137 0.134
73 29 8 4682.77 4700.141 0.107 0.104
74 34 7 4792.20 4807.568 0.086 0.083
75 11 6 4921.47 4934.784 0.062 0.059
76 30 5 4951.47 4962.377 0.056 0.054
77 64 4 4963.49 4971.937 0.054 0.052
78 52 3 5024.68 5030.718 0.042 0.041
79 39 2 5095.04 5098.605 0.028 0.028
80 48 1 5244.48 5245.526 0.000 0.000
--------------------------------------------------
Selected iteration: 24
Forward Pass
---------------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
---------------------------------------------------------------------
0 - - - 5244.476631 1 5245.526 0.000 0.000
1 0 6 9961 5067.564966 3 5073.652 0.034 0.033
2 2 6 3206 4861.646322 5 4872.360 0.073 0.071
3 4 6 7844 4639.910399 7 4654.794 0.115 0.113
4 0 6 7260 4468.624616 9 4487.452 0.148 0.145
5 7 6 8157 4244.467266 11 4266.625 0.191 0.187
6 9 6 2242 3900.087914 13 3924.381 0.256 0.252
7 10 6 5832 3770.802883 15 3798.100 0.281 0.276
8 7 6 1644 3534.771940 17 3563.936 0.326 0.321
9 15 6 3475 3314.407980 19 3345.112 0.368 0.362
10 15 6 2648 3162.265769 21 3194.769 0.397 0.391
11 9 6 1923 3028.741358 23 3062.950 0.422 0.416
12 7 6 3624 2880.064377 25 2915.525 0.451 0.444
13 23 6 3486 2702.824122 27 2738.858 0.485 0.478
14 23 6 116 2545.534016 29 2582.069 0.515 0.508
15 4 6 8773 2422.575970 31 2459.823 0.538 0.531
16 2 6 803 2262.126670 33 2299.223 0.569 0.562
17 32 6 5864 2122.594794 35 2159.580 0.595 0.588
18 4 6 7610 1836.777669 37 1870.669 0.650 0.643
19 0 6 2035 1641.898343 39 1673.883 0.687 0.681
20 38 6 7332 1428.554810 41 1457.855 0.728 0.722
21 40 6 9013 1053.447265 43 1076.141 0.799 0.795
22 37 6 1206 758.322249 45 775.442 0.855 0.852
23 7 6 593 636.565160 47 651.594 0.879 0.876
24 43 6 6001 532.755707 49 545.886 0.898 0.896
25 23 6 1488 451.992938 51 463.602 0.914 0.912
26 37 6 6122 385.157239 53 395.450 0.927 0.925
27 7 6 6946 335.936149 55 345.263 0.936 0.934
28 32 6 3381 287.101417 57 295.372 0.945 0.944
29 24 6 1440 235.668475 59 242.704 0.955 0.954
30 32 6 8375 209.747432 61 216.228 0.960 0.959
31 45 6 500 196.500438 63 202.778 0.963 0.961
32 2 6 3553 184.151662 65 190.228 0.965 0.964
33 39 6 9809 173.669012 67 179.582 0.967 0.966
34 52 6 1334 161.396838 69 167.061 0.969 0.968
35 9 6 1940 154.513111 71 160.099 0.971 0.969
36 7 6 9087 147.735445 73 153.232 0.972 0.971
37 53 6 3475 141.226286 75 146.630 0.973 0.972
38 40 6 1097 135.344070 77 140.666 0.974 0.973
39 40 6 7450 129.288718 79 134.510 0.975 0.974
40 64 6 1948 124.662704 81 129.829 0.976 0.975
---------------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Pruning Pass
--------------------------------------------------
iter bf terms mse gcv rsq grsq
--------------------------------------------------
0 - 81 124.94 130.113 0.976 0.975
1 43 80 124.94 130.047 0.976 0.975
2 31 79 124.94 129.981 0.976 0.975
3 35 78 124.94 129.915 0.976 0.975
4 1 77 124.94 129.848 0.976 0.975
5 58 76 124.94 129.782 0.976 0.975
6 17 75 124.94 129.716 0.976 0.975
7 40 74 124.94 129.650 0.976 0.975
8 63 73 124.94 129.584 0.976 0.975
9 69 72 124.94 129.518 0.976 0.975
10 42 71 124.94 129.452 0.976 0.975
11 46 70 124.94 129.386 0.976 0.975
12 26 69 124.94 129.320 0.976 0.975
13 23 68 124.94 129.255 0.976 0.975
14 71 67 124.94 129.189 0.976 0.975
15 55 66 124.94 129.123 0.976 0.975
16 15 65 124.94 129.058 0.976 0.975
17 60 64 124.94 128.992 0.976 0.975
18 54 63 124.94 128.927 0.976 0.975
19 9 62 124.94 128.861 0.976 0.975
20 6 61 124.94 128.796 0.976 0.975
21 10 60 124.93 128.723 0.976 0.975
22 13 59 124.93 128.662 0.976 0.975
23 8 58 124.94 128.604 0.976 0.975
24 16 57 124.99 128.586 0.976 0.975
25 4 56 125.10 128.642 0.976 0.975
26 32 55 125.61 129.095 0.976 0.975
27 33 54 127.52 130.994 0.976 0.975
28 74 53 128.99 132.437 0.975 0.975
29 80 52 131.21 134.645 0.975 0.974
30 22 51 132.74 136.150 0.975 0.974
31 21 50 133.34 136.691 0.975 0.974
32 75 49 133.99 137.295 0.974 0.974
33 36 48 138.74 142.089 0.974 0.973
34 79 47 144.86 148.276 0.972 0.972
35 72 46 151.28 154.769 0.971 0.970
36 70 45 160.51 164.129 0.969 0.969
37 66 44 170.02 173.767 0.968 0.967
38 65 43 178.52 182.365 0.966 0.965
39 25 42 188.91 192.887 0.964 0.963
40 68 41 199.78 203.874 0.962 0.961
41 7 40 211.71 215.947 0.960 0.959
42 59 39 223.54 227.893 0.957 0.957
43 45 38 240.03 244.579 0.954 0.953
44 76 37 252.64 257.300 0.952 0.951
45 67 36 277.68 282.664 0.947 0.946
46 5 35 307.60 312.958 0.941 0.940
47 62 34 339.68 345.429 0.935 0.934
48 61 33 349.66 355.399 0.933 0.932
49 56 32 406.73 413.191 0.922 0.921
50 53 31 476.86 484.187 0.909 0.908
51 73 30 531.86 539.769 0.899 0.897
52 19 29 565.68 573.801 0.892 0.891
53 3 28 724.42 734.443 0.862 0.860
54 20 27 974.98 987.983 0.814 0.812
55 57 26 1241.03 1256.947 0.763 0.760
56 18 25 1547.42 1566.472 0.705 0.701
57 14 24 1934.24 1957.075 0.631 0.627
58 44 23 2135.76 2159.880 0.593 0.588
59 38 22 2283.01 2307.631 0.565 0.560
60 49 21 2339.81 2363.860 0.554 0.549
61 27 20 2504.83 2529.307 0.522 0.518
62 12 19 2702.93 2727.972 0.485 0.480
63 24 18 2955.40 2981.280 0.436 0.432
64 50 17 3260.70 3287.600 0.378 0.373
65 28 16 3372.40 3398.523 0.357 0.352
66 41 15 3598.03 3624.073 0.314 0.309
67 51 14 3906.02 3932.321 0.255 0.250
68 37 13 3982.16 4006.966 0.241 0.236
69 2 12 4090.99 4114.409 0.220 0.216
70 78 11 4427.86 4450.979 0.156 0.151
71 47 10 4472.96 4494.060 0.147 0.143
72 77 9 4524.47 4543.529 0.137 0.134
73 29 8 4682.77 4700.141 0.107 0.104
74 34 7 4792.20 4807.568 0.086 0.083
75 11 6 4921.47 4934.784 0.062 0.059
76 30 5 4951.47 4962.377 0.056 0.054
77 64 4 4963.49 4971.937 0.054 0.052
78 52 3 5024.68 5030.718 0.042 0.041
79 39 2 5095.04 5098.605 0.028 0.028
80 48 1 5244.48 5245.526 0.000 0.000
--------------------------------------------------
Selected iteration: 24
Earth Model
------------------------------------------------------------------
Basis Function Pruned Coefficient
------------------------------------------------------------------
(Intercept) No -803005
h(x6-37.2487) Yes None
h(37.2487-x6) No 188.026
h(x6-34.6929)*h(37.2487-x6) No -57.3172
h(34.6929-x6)*h(37.2487-x6) No -14.598
h(x6-31.4766)*h(34.6929-x6)*h(37.2487-x6) No 7.22891
h(31.4766-x6)*h(34.6929-x6)*h(37.2487-x6) Yes None
h(x6+37.1733) No 2791.92
h(-37.1733-x6) Yes None
h(x6+30.3035)*h(x6+37.1733) Yes None
h(-30.3035-x6)*h(x6+37.1733) Yes None
h(x6+24.4224)*h(x6+30.3035)*h(x6+37.1733) No 6.74221
h(-24.4224-x6)*h(x6+30.3035)*h(x6+37.1733) No -8.02723
h(x6+32.6468)*h(-30.3035-x6)*h(x6+37.1733) Yes None
h(-32.6468-x6)*h(-30.3035-x6)*h(x6+37.1733) No 17.9338
h(x6+21.4336)*h(x6+37.1733) Yes None
h(-21.4336-x6)*h(x6+37.1733) Yes None
h(x6+18.9904)*h(x6+21.4336)*h(x6+37.1733) Yes None
h(-18.9904-x6)*h(x6+21.4336)*h(x6+37.1733) No -5.59185
h(x6+15.1619)*h(x6+21.4336)*h(x6+37.1733) No -2.09208
h(-15.1619-x6)*h(x6+21.4336)*h(x6+37.1733) No 2.522
h(x6+11.6831)*h(x6+30.3035)*h(x6+37.1733) No -1.52138
h(-11.6831-x6)*h(x6+30.3035)*h(x6+37.1733) No 1.45609
h(x6+8.85579)*h(x6+37.1733) Yes None
h(-8.85579-x6)*h(x6+37.1733) No -114.6
h(x6+6.44975)*h(x6+8.85579)*h(x6+37.1733) No -1.13963
h(-6.44975-x6)*h(x6+8.85579)*h(x6+37.1733) Yes None
h(x6+2.53505)*h(x6+8.85579)*h(x6+37.1733) No -48.1755
h(-2.53505-x6)*h(x6+8.85579)*h(x6+37.1733) No 48.6257
h(x6-27.8323)*h(34.6929-x6)*h(37.2487-x6) No 4.21319
h(27.8323-x6)*h(34.6929-x6)*h(37.2487-x6) No -5.01954
h(x6-24.2978)*h(37.2487-x6) Yes None
h(24.2978-x6)*h(37.2487-x6) No -7.6801
h(x6-17.967)*h(24.2978-x6)*h(37.2487-x6) No -2.12423
h(17.967-x6)*h(24.2978-x6)*h(37.2487-x6) No 4.57391
h(x6-14.9965)*h(34.6929-x6)*h(37.2487-x6) Yes None
h(14.9965-x6)*h(34.6929-x6)*h(37.2487-x6) No 0.751507
h(x6-11.4815) No -59690.4
h(11.4815-x6) No 46789.7
h(x6-5.48349)*h(11.4815-x6) No 1021.09
h(5.48349-x6)*h(11.4815-x6) Yes None
h(x6+1.02101)*h(5.48349-x6)*h(11.4815-x6) No 2.90161
h(-1.02101-x6)*h(5.48349-x6)*h(11.4815-x6) Yes None
h(x6-24.4123)*h(x6-11.4815) Yes None
h(24.4123-x6)*h(x6-11.4815) No -32.4221
h(x6+16.989)*h(x6+37.1733) No 23.3009
h(-16.989-x6)*h(x6+37.1733) Yes None
h(x6-29.1534)*h(x6-24.4123)*h(x6-11.4815) No -9.5744
h(29.1534-x6)*h(x6-24.4123)*h(x6-11.4815) No 10.0986
h(x6+4.90451)*h(x6+8.85579)*h(x6+37.1733) No 48.9149
h(-4.90451-x6)*h(x6+8.85579)*h(x6+37.1733) No -49.8358
h(x6-17.8314)*h(x6-11.4815) No -1186.75
h(17.8314-x6)*h(x6-11.4815) No 1193.17
h(x6+26.7124)*h(x6+37.1733) No 18.2946
h(-26.7124-x6)*h(x6+37.1733) Yes None
h(x6-3.83896)*h(24.2978-x6)*h(37.2487-x6) Yes None
h(3.83896-x6)*h(24.2978-x6)*h(37.2487-x6) No 0.223623
h(x6+13.5093)*h(-8.85579-x6)*h(x6+37.1733) No 1.36938
h(-13.5093-x6)*h(-8.85579-x6)*h(x6+37.1733) Yes None
h(x6-19.0415)*h(24.2978-x6)*h(37.2487-x6) No 1.72457
h(19.0415-x6)*h(24.2978-x6)*h(37.2487-x6) Yes None
h(x6-0.224416)*h(x6+16.989)*h(x6+37.1733) No 1.68078
h(0.224416-x6)*h(x6+16.989)*h(x6+37.1733) No -1.6004
h(x6-30.2116)*h(37.2487-x6) Yes None
h(30.2116-x6)*h(37.2487-x6) No 27.0289
h(x6-8.16867)*h(x6-5.48349)*h(11.4815-x6) No -3.1417
h(8.16867-x6)*h(x6-5.48349)*h(11.4815-x6) No -5.95814
h(x6-14.9373)*h(17.8314-x6)*h(x6-11.4815) No -16.2685
h(14.9373-x6)*h(17.8314-x6)*h(x6-11.4815) No -12.5622
h(x6+28.1102)*h(x6+30.3035)*h(x6+37.1733) Yes None
h(-28.1102-x6)*h(x6+30.3035)*h(x6+37.1733) No 5.21693
h(x6+23.3288)*h(x6+37.1733) Yes None
h(-23.3288-x6)*h(x6+37.1733) No -5.72154
h(x6+18.9904)*h(x6+26.7124)*h(x6+37.1733) No 2.81992
h(-18.9904-x6)*h(x6+26.7124)*h(x6+37.1733) No -1.14742
h(x6-3.90363)*h(5.48349-x6)*h(11.4815-x6) No 12.6573
h(3.90363-x6)*h(5.48349-x6)*h(11.4815-x6) No -21.5864
h(x6+32.6274)*h(5.48349-x6)*h(11.4815-x6) No -27.0684
h(-32.6274-x6)*h(5.48349-x6)*h(11.4815-x6) No 26.9698
h(x6-26.9536)*h(30.2116-x6)*h(37.2487-x6) No -3.53026
h(26.9536-x6)*h(30.2116-x6)*h(37.2487-x6) No 1.29164
------------------------------------------------------------------
MSE: 124.9852, GCV: 128.5858, RSQ: 0.9762, GRSQ: 0.9755
import numpy
import matplotlib.pyplot as plt
from pyearth import Earth
# Create some fake data
numpy.random.seed(2)
m = 10000
n = 10
X = 80 * numpy.random.uniform(size=(m, n)) - 40
y = 100 * \
(numpy.sin((X[:, 6])) - 4.0) + \
10 * numpy.random.normal(size=m)
# Fit an Earth model
model = Earth(max_degree=3, minspan_alpha=.5, verbose=True)
model.fit(X, y)
# Print the model
print(model.trace())
print(model.summary())
# Plot the model
y_hat = model.predict(X)
plt.plot(X[:, 6], y, 'r.')
plt.plot(X[:, 6], y_hat, 'b.')
plt.show()
Total running time of the script: (4 minutes 14.485 seconds)
Download Python source code:
plot_sine_wave.py
Download IPython notebook:
plot_sine_wave.ipynb