Plotting derivatives of simple sine function¶
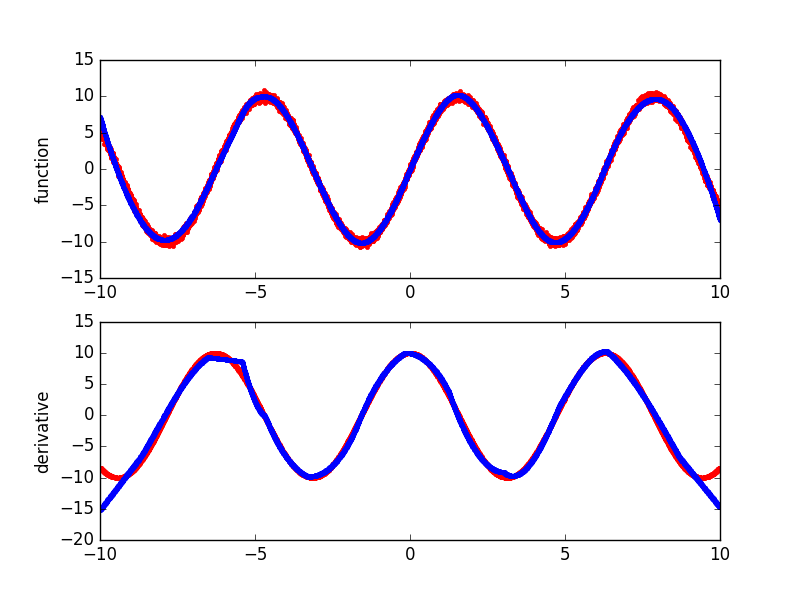
A simple example plotting a fit of the sine function and the derivatives computed by Earth.
Out:
Forward Pass
-----------------------------------------------------------------
iter parent var knot mse terms gcv rsq grsq
-----------------------------------------------------------------
0 - - - 47.918854 1 47.928 0.000 0.000
1 0 6 6267 44.373430 3 44.427 0.074 0.073
2 1 6 910 36.297242 5 36.377 0.243 0.241
3 2 6 5630 21.514715 7 21.584 0.551 0.550
4 0 6 2975 10.917076 9 10.963 0.772 0.771
5 8 6 2991 3.708183 11 3.728 0.923 0.922
6 7 6 2577 1.509533 13 1.519 0.968 0.968
7 1 6 1569 0.882026 15 0.888 0.982 0.981
8 2 6 264 0.577276 17 0.582 0.988 0.988
9 0 6 4442 0.313841 19 0.317 0.993 0.993
10 0 6 4497 0.232471 21 0.235 0.995 0.995
11 20 6 4242 0.190910 23 0.193 0.996 0.996
-----------------------------------------------------------------
Stopping Condition 2: Improvement below threshold
Pruning Pass
----------------------------------------------
iter bf terms mse gcv rsq grsq
----------------------------------------------
0 - 23 0.19 0.193 0.996 0.996
1 10 22 0.19 0.193 0.996 0.996
2 20 21 0.19 0.193 0.996 0.996
3 15 20 0.19 0.193 0.996 0.996
4 8 19 0.19 0.193 0.996 0.996
5 18 18 0.19 0.193 0.996 0.996
6 14 17 0.19 0.192 0.996 0.996
7 12 16 0.19 0.193 0.996 0.996
8 5 15 0.19 0.193 0.996 0.996
9 22 14 0.19 0.195 0.996 0.996
10 6 13 0.20 0.196 0.996 0.996
11 1 12 0.24 0.239 0.995 0.995
12 4 11 0.24 0.242 0.995 0.995
13 7 10 0.29 0.290 0.994 0.994
14 3 9 0.52 0.523 0.989 0.989
15 13 8 0.68 0.682 0.986 0.986
16 11 7 9.35 9.382 0.805 0.804
17 19 6 17.56 17.603 0.634 0.633
18 17 5 20.15 20.192 0.580 0.579
19 16 4 26.45 26.491 0.448 0.447
20 2 3 32.32 32.360 0.326 0.325
21 21 2 42.58 42.615 0.111 0.111
22 9 1 47.92 47.928 0.000 0.000
----------------------------------------------
Selected iteration: 6
Earth Model
--------------------------------------------------------------------------------------------------
Basis Function Pruned Coefficient
--------------------------------------------------------------------------------------------------
(Intercept) No 44.8098
C(x6|s=+1,-5.41239,-5.16768,-4.67412) No -26.6867
C(x6|s=-1,-5.41239,-5.16768,-4.67412) No 31.9844
C(x6|s=+1,-0.137739,0.751892,1.25163)*C(x6|s=+1,-5.41239,-5.16768,-4.67412) No 0.909836
C(x6|s=-1,-0.137739,0.751892,1.25163)*C(x6|s=+1,-5.41239,-5.16768,-4.67412) No -1.83328
C(x6|s=+1,-6.49945,-5.65709,-5.41239)*C(x6|s=-1,-5.41239,-5.16768,-4.67412) No -2.86683
C(x6|s=-1,-6.49945,-5.65709,-5.41239)*C(x6|s=-1,-5.41239,-5.16768,-4.67412) No 3.05546
C(x6|s=+1,3.01553,4.27971,4.81202) No -5.61853
C(x6|s=-1,3.01553,4.27971,4.81202) Yes None
C(x6|s=+1,-1.70957,-1.02737,-0.137739)*C(x6|s=-1,3.01553,4.27971,4.81202) No 1.74983
C(x6|s=-1,-1.70957,-1.02737,-0.137739)*C(x6|s=-1,3.01553,4.27971,4.81202) Yes None
C(x6|s=+1,6.35128,7.35822,8.67854)*C(x6|s=+1,3.01553,4.27971,4.81202) No -6.60667
C(x6|s=-1,6.35128,7.35822,8.67854)*C(x6|s=+1,3.01553,4.27971,4.81202) No 4.12412
C(x6|s=+1,-3.28616,-2.39176,-1.70957)*C(x6|s=+1,-5.41239,-5.16768,-4.67412) No 2.62654
C(x6|s=-1,-3.28616,-2.39176,-1.70957)*C(x6|s=+1,-5.41239,-5.16768,-4.67412) Yes None
C(x6|s=+1,-8.6707,-7.34181,-6.49945)*C(x6|s=-1,-5.41239,-5.16768,-4.67412) Yes None
C(x6|s=-1,-8.6707,-7.34181,-6.49945)*C(x6|s=-1,-5.41239,-5.16768,-4.67412) No 3.58191
C(x6|s=+1,1.25163,1.75136,3.01553) No -9.68315
C(x6|s=-1,1.25163,1.75136,3.01553) Yes None
C(x6|s=+1,4.81202,5.34433,6.35128) No -12.1327
C(x6|s=-1,4.81202,5.34433,6.35128) Yes None
C(x6|s=+1,-4.67412,-4.18056,-3.28616)*C(x6|s=-1,4.81202,5.34433,6.35128) No 2.68856
C(x6|s=-1,-4.67412,-4.18056,-3.28616)*C(x6|s=-1,4.81202,5.34433,6.35128) No -3.3853
--------------------------------------------------------------------------------------------------
MSE: 0.1448, GCV: 0.1460, RSQ: 0.9970, GRSQ: 0.9970
import numpy
import matplotlib.pyplot as plt
from pyearth import Earth
# Create some fake data
numpy.random.seed(2)
m = 10000
n = 10
X = 20 * numpy.random.uniform(size=(m, n)) - 10
y = 10*numpy.sin(X[:, 6]) + 0.25*numpy.random.normal(size=m)
# Compute the known true derivative with respect to the predictive variable
y_prime = 10*numpy.cos(X[:, 6])
# Fit an Earth model
model = Earth(max_degree=2, minspan_alpha=.5, smooth=True)
model.fit(X, y)
# Print the model
print(model.trace())
print(model.summary())
# Get the predicted values and derivatives
y_hat = model.predict(X)
y_prime_hat = model.predict_deriv(X, 'x6')
# Plot true and predicted function values and derivatives
# for the predictive variable
plt.subplot(211)
plt.plot(X[:, 6], y, 'r.')
plt.plot(X[:, 6], y_hat, 'b.')
plt.ylabel('function')
plt.subplot(212)
plt.plot(X[:, 6], y_prime, 'r.')
plt.plot(X[:, 6], y_prime_hat[:, 0], 'b.')
plt.ylabel('derivative')
plt.show()
Total running time of the script: (0 minutes 7.862 seconds)
Download Python source code:
plot_derivatives.py
Download IPython notebook:
plot_derivatives.ipynb