Sensitivity to hyper-parameters in SVRG

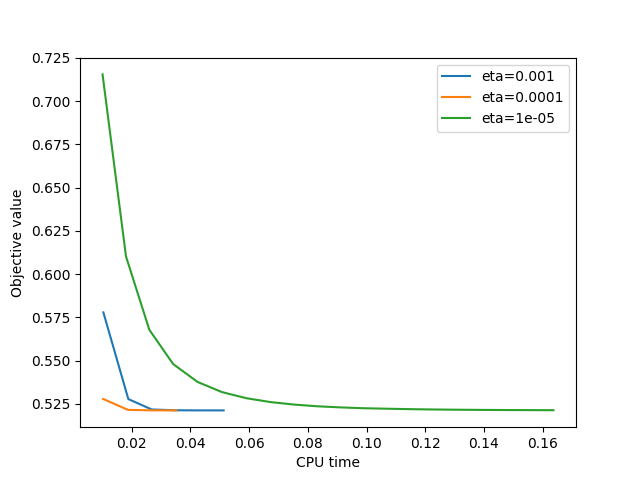
This example shows the sensitivity of SVRG with respect to different hyperparameters.

• 
• 

Out:

eta = 0.001
eta = 0.0001
eta = 1e-05
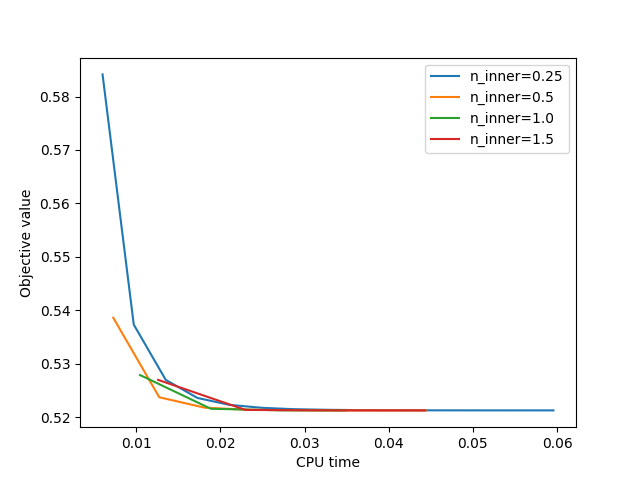
n_inner = 0.25
n_inner = 0.5
n_inner = 1.0
n_inner = 1.5

print(__doc__)

import sys
import time

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_classification
from sklearn.datasets import fetch_20newsgroups_vectorized

from lightning.classification import SVRGClassifier


class Callback(object):

    def __init__(self, X, y):
        self.X = X
        self.y = y
        self.obj = []
        self.times = []
        self.start_time = time.time()
        self.test_time = 0

    def __call__(self, clf):
        test_time = time.time()
        clf._finalize_coef()
        y_pred = clf.decision_function(self.X).ravel()
        loss = (np.maximum(1 - self.y * y_pred, 0) ** 2).mean()
        coef = clf.coef_.ravel()
        regul = 0.5 * clf.alpha * np.dot(coef, coef)
        self.obj.append(loss + regul)
        self.test_time += time.time() - test_time
        self.times.append(time.time() -  self.start_time - self.test_time)

try:
    dataset = sys.argv[1]
except:
    dataset = "synthetic"

if dataset == "news20":
    bunch = fetch_20newsgroups_vectorized(subset="all")
    X = bunch.data
    y = bunch.target
    y[y >= 1] = 1

    etas = (0.5, 1e-1, 1e-2)
    n_inners = (1.0, 2.0, 3.0)
else:
    X, y = make_classification(n_samples=10000,
                               n_features=100,
                               n_classes=2,
                               random_state=0)
    etas = (1e-3, 1e-4, 1e-5)
    n_inners = (0.25, 0.5, 1.0, 1.5)

y = y * 2 - 1


plt.figure()

for eta in etas:
    print("eta =", eta)
    cb = Callback(X, y)
    clf = SVRGClassifier(loss="squared_hinge", alpha=1e-5, eta=eta,
                         n_inner=1.0, max_iter=20, random_state=0, callback=cb)
    clf.fit(X, y)
    plt.plot(cb.times, cb.obj, label="eta=" + str(eta))

plt.xlabel("CPU time")
plt.ylabel("Objective value")
plt.legend()

plt.figure()

for n_inner in n_inners:
    print("n_inner =", n_inner)
    cb = Callback(X, y)
    clf = SVRGClassifier(loss="squared_hinge", alpha=1e-5, eta=1e-4,
                         n_inner=n_inner, max_iter=20, random_state=0,
                         callback=cb)
    clf.fit(X, y)
    plt.plot(cb.times, cb.obj, label="n_inner=" + str(n_inner))

plt.xlabel("CPU time")
plt.ylabel("Objective value")
plt.legend()

plt.show()