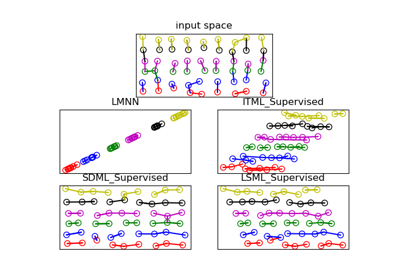
`metric_learn`.LMNN

class metric_learn.LMNN(init='auto', n_neighbors=3, min_iter=50, max_iter=1000, learn_rate=1e-07, regularization=0.5, convergence_tol=0.001, verbose=False, preprocessor=None, n_components=None, random_state=None, k='deprecated')[source]

Large Margin Nearest Neighbor (LMNN)

LMNN learns a Mahalanobis distance metric in the kNN classification setting. The learned metric attempts to keep close k-nearest neighbors from the same class, while keeping examples from different classes separated by a large margin. This algorithm makes no assumptions about the distribution of the data.

Read more in the User Guide.

Parameters:

initstring or numpy array, optional (default=’auto’)

Initialization of the linear transformation. Possible options are ‘auto’, ‘pca’, ‘identity’, ‘random’, and a numpy array of shape (n_features_a, n_features_b).

‘auto’: Depending on n_components, the most reasonable initialization will be chosen. If n_components <= n_classes we use ‘lda’, as it uses labels information. If not, but n_components < min(n_features, n_samples), we use ‘pca’, as it projects data in meaningful directions (those of higher variance). Otherwise, we just use ‘identity’.
‘pca’: n_components principal components of the inputs passed to fit() will be used to initialize the transformation. (See sklearn.decomposition.PCA)
‘lda’: min(n_components, n_classes) most discriminative components of the inputs passed to fit() will be used to initialize the transformation. (If n_components > n_classes, the rest of the components will be zero.) (See sklearn.discriminant_analysis.LinearDiscriminantAnalysis)
‘identity’: If n_components is strictly smaller than the dimensionality of the inputs passed to fit(), the identity matrix will be truncated to the first n_components rows.
‘random’: The initial transformation will be a random array of shape (n_components, n_features). Each value is sampled from the standard normal distribution.
numpy array: n_features_b must match the dimensionality of the inputs passed to fit() and n_features_a must be less than or equal to that. If n_components is not None, n_features_a must match it.

n_neighborsint, optional (default=3)

Number of neighbors to consider, not including self-edges.

min_iterint, optional (default=50)

Minimum number of iterations of the optimization procedure.

max_iterint, optional (default=1000)

Maximum number of iterations of the optimization procedure.

learn_ratefloat, optional (default=1e-7)

Learning rate of the optimization procedure

tolfloat, optional (default=0.001)

Tolerance of the optimization procedure. If the objective value varies less than tol, we consider the algorithm has converged and stop it.

verbosebool, optional (default=False)

Whether to print the progress of the optimization procedure.

regularization: float, optional (default=0.5)

Relative weight between pull and push terms, with 0.5 meaning equal weight.

preprocessorarray-like, shape=(n_samples, n_features) or callable

The preprocessor to call to get tuples from indices. If array-like, tuples will be formed like this: X[indices].

n_componentsint or None, optional (default=None)

Dimensionality of reduced space (if None, defaults to dimension of X).

random_stateint or numpy.RandomState or None, optional (default=None)

A pseudo random number generator object or a seed for it if int. If init='random', random_state is used to initialize the random transformation. If init='pca', random_state is passed as an argument to PCA when initializing the transformation.

kRenamed to n_neighbors. Will be deprecated in 0.7.0

References

[1]

K. Q. Weinberger, J. Blitzer, L. K. Saul. Distance Metric Learning for Large Margin Nearest Neighbor Classification. NIPS 2005.

Examples

>>> import numpy as np
>>> from metric_learn import LMNN
>>> from sklearn.datasets import load_iris
>>> iris_data = load_iris()
>>> X = iris_data['data']
>>> Y = iris_data['target']
>>> lmnn = LMNN(n_neighbors=5, learn_rate=1e-6)
>>> lmnn.fit(X, Y, verbose=False)

Attributes:

n_iter_int: The number of iterations the solver has run.
components_numpy.ndarray, shape=(n_components, n_features): The learned linear transformation L.

Methods

`fit_transform`(X[, y])	Fit to data, then transform it.
`get_mahalanobis_matrix`()	Returns a copy of the Mahalanobis matrix learned by the metric learner.
`get_metadata_routing`()	Get metadata routing of this object.
`get_metric`()	Returns a function that takes as input two 1D arrays and outputs the value of the learned metric on these two points.
`get_params`([deep])	Get parameters for this estimator.
`pair_distance`(pairs)	Returns the learned Mahalanobis distance between pairs.
`pair_score`(pairs)	Returns the opposite of the learned Mahalanobis distance between pairs.
`score_pairs`(pairs)	Returns the learned Mahalanobis distance between pairs.
`set_output`(*[, transform])	Set output container.
`set_params`(**params)	Set the parameters of this estimator.
`transform`(X)	Embeds data points in the learned linear embedding space.

fit

__init__(init='auto', n_neighbors=3, min_iter=50, max_iter=1000, learn_rate=1e-07, regularization=0.5, convergence_tol=0.001, verbose=False, preprocessor=None, n_components=None, random_state=None, k='deprecated')[source]

fit(X, y)[source]

fit_transform(X, y=None, **fit_params)

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:

Xarray-like of shape (n_samples, n_features): Input samples.
yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None: Target values (None for unsupervised transformations).
**fit_paramsdict: Additional fit parameters.

Returns:

X_newndarray array of shape (n_samples, n_features_new): Transformed array.

get_mahalanobis_matrix()

Returns a copy of the Mahalanobis matrix learned by the metric learner.

Returns:

Mnumpy.ndarray, shape=(n_features, n_features): The copy of the learned Mahalanobis matrix.

get_metadata_routing()

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest: A MetadataRequest encapsulating routing information.

get_metric()

Returns a function that takes as input two 1D arrays and outputs the value of the learned metric on these two points. Depending on the algorithm, it can return a distance or a similarity function between pairs.

This function will be independent from the metric learner that learned it (it will not be modified if the initial metric learner is modified), and it can be directly plugged into the metric argument of scikit-learn’s estimators.

Returns:

metric_funfunction: The function described above.

See also

pair_distance: a method that returns the distance between several pairs of points. Unlike get_metric, this is a method of the metric learner and therefore can change if the metric learner changes. Besides, it can use the metric learner’s preprocessor, and works on concatenated arrays.
pair_score: a method that returns the similarity score between several pairs of points. Unlike get_metric, this is a method of the metric learner and therefore can change if the metric learner changes. Besides, it can use the metric learner’s preprocessor, and works on concatenated arrays.

Examples

>>> from metric_learn import NCA
>>> from sklearn.datasets import make_classification
>>> from sklearn.neighbors import KNeighborsClassifier
>>> nca = NCA()
>>> X, y = make_classification()
>>> nca.fit(X, y)
>>> knn = KNeighborsClassifier(metric=nca.get_metric())
>>> knn.fit(X, y) 
KNeighborsClassifier(algorithm='auto', leaf_size=30,
  metric=<function MahalanobisMixin.get_metric.<locals>.metric_fun
          at 0x...>,
  metric_params=None, n_jobs=None, n_neighbors=5, p=2,
  weights='uniform')

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

pair_distance(pairs)

Returns the learned Mahalanobis distance between pairs.

This distance is defined as: \(d_M(x, x') = \sqrt{(x-x')^T M (x-x')}\) where M is the learned Mahalanobis matrix, for every pair of points x and x'. This corresponds to the euclidean distance between embeddings of the points in a new space, obtained through a linear transformation. Indeed, we have also: \(d_M(x, x') = \sqrt{(x_e - x_e')^T (x_e- x_e')}\), with \(x_e = L x\) (See MahalanobisMixin).

Parameters:

pairsarray-like, shape=(n_pairs, 2, n_features) or (n_pairs, 2): 3D Array of pairs to score, with each row corresponding to two points, for 2D array of indices of pairs if the metric learner uses a preprocessor.

Returns:

scoresnumpy.ndarray of shape=(n_pairs,): The learned Mahalanobis distance for every pair.

See also

get_metric: a method that returns a function to compute the metric between two points. The difference with pair_distance is that it works on two 1D arrays and cannot use a preprocessor. Besides, the returned function is independent of the metric learner and hence is not modified if the metric learner is.
Mahalanobis Distances: The section of the project documentation that describes Mahalanobis Distances.

pair_score(pairs)

Returns the opposite of the learned Mahalanobis distance between pairs.

Parameters:

pairsarray-like, shape=(n_pairs, 2, n_features) or (n_pairs, 2): 3D Array of pairs to score, with each row corresponding to two points, for 2D array of indices of pairs if the metric learner uses a preprocessor.

Returns:

scoresnumpy.ndarray of shape=(n_pairs,): The opposite of the learned Mahalanobis distance for every pair.

See also

get_metric: a method that returns a function to compute the metric between two points. The difference with pair_score is that it works on two 1D arrays and cannot use a preprocessor. Besides, the returned function is independent of the metric learner and hence is not modified if the metric learner is.
Mahalanobis Distances: The section of the project documentation that describes Mahalanobis Distances.

score_pairs(pairs)

Returns the learned Mahalanobis distance between pairs.

This distance is defined as: \(d_M(x, x') = \\sqrt{(x-x')^T M (x-x')}\) where M is the learned Mahalanobis matrix, for every pair of points x and x'. This corresponds to the euclidean distance between embeddings of the points in a new space, obtained through a linear transformation. Indeed, we have also: \(d_M(x, x') = \\sqrt{(x_e - x_e')^T (x_e- x_e')}\), with \(x_e = L x\) (See MahalanobisMixin).

Deprecated since version 0.7.0: Please use pair_distance instead.

Warning

This method will be removed in 0.8.0. Please refer to pair_distance or pair_score. This change will occur in order to add learners that don’t necessarily learn a Mahalanobis distance.

Parameters:

pairsarray-like, shape=(n_pairs, 2, n_features) or (n_pairs, 2): 3D Array of pairs to score, with each row corresponding to two points, for 2D array of indices of pairs if the metric learner uses a preprocessor.

Returns:

scoresnumpy.ndarray of shape=(n_pairs,): The learned Mahalanobis distance for every pair.

See also

get_metric: a method that returns a function to compute the metric between two points. The difference with score_pairs is that it works on two 1D arrays and cannot use a preprocessor. Besides, the returned function is independent of the metric learner and hence is not modified if the metric learner is.
Mahalanobis Distances: The section of the project documentation that describes Mahalanobis Distances.

set_output(*, transform=None)

Set output container.

See Introducing the set_output API for an example on how to use the API.

Parameters:

transform{“default”, “pandas”}, default=None

Configure output of transform and fit_transform.

“default”: Default output format of a transformer
“pandas”: DataFrame output
None: Transform configuration is unchanged

Returns:

selfestimator instance: Estimator instance.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

transform(X)

Embeds data points in the learned linear embedding space.

Transforms samples in X into X_embedded, samples inside a new embedding space such that: X_embedded = X.dot(L.T), where L is the learned linear transformation (See MahalanobisMixin).

Parameters:

Xnumpy.ndarray, shape=(n_samples, n_features): The data points to embed.

Returns:

X_embeddednumpy.ndarray, shape=(n_samples, n_components): The embedded data points.

Examples using `metric_learn.LMNN`

Sandwich demo

Algorithms walkthrough

metric_learn.LMNN

Examples using metric_learn.LMNN

`metric_learn`.LMNN

Examples using `metric_learn.LMNN`