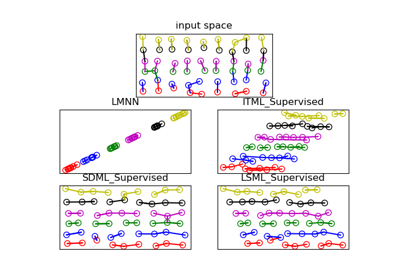
`metric_learn`.ITML_Supervised

class metric_learn.ITML_Supervised(gamma=1.0, max_iter=1000, tol=0.001, n_constraints=None, prior='identity', verbose=False, preprocessor=None, random_state=None, num_constraints='deprecated', convergence_threshold='deprecated')[source]

Supervised version of Information Theoretic Metric Learning (ITML)

ITML_Supervised creates pairs of similar sample by taking same class samples, and pairs of dissimilar samples by taking different class samples. It then passes these pairs to ITML for training.

Parameters:

gammafloat, optional (default=1.0)

Value for slack variables

max_iterint, optional (default=1000)

Maximum number of iterations of the optimization procedure.

tolfloat, optional (default=1e-3)

Tolerance of the optimization procedure.

n_constraintsint, optional (default=None)

Number of constraints to generate. If None, default to 20 * num_classes**2.

priorstring or numpy array, optional (default=’identity’)

Initialization of the Mahalanobis matrix. Possible options are ‘identity’, ‘covariance’, ‘random’, and a numpy array of shape (n_features, n_features). For ITML, the prior should be strictly positive definite (PD).

‘identity’: An identity matrix of shape (n_features, n_features).
‘covariance’: The inverse covariance matrix.
‘random’: The prior will be a random SPD matrix of shape (n_features, n_features), generated using sklearn.datasets.make_spd_matrix.
numpy array: A positive definite (PD) matrix of shape (n_features, n_features), that will be used as such to set the prior.

verbosebool, optional (default=False)

If True, prints information while learning

preprocessorarray-like, shape=(n_samples, n_features) or callable

The preprocessor to call to get tuples from indices. If array-like, tuples will be formed like this: X[indices].

random_stateint or numpy.RandomState or None, optional (default=None)

A pseudo random number generator object or a seed for it if int. If prior='random', random_state is used to set the prior. In any case, random_state is also used to randomly sample constraints from labels.

num_constraintsRenamed to n_constraints. Will be deprecated in 0.7.0

convergence_thresholdRenamed to tol. Will be deprecated in 0.7.0

See also

metric_learn.ITML: The original weakly-supervised algorithm
Supervised versions of weakly-supervised algorithms: The section of the project documentation that describes the supervised version of weakly supervised estimators.

Examples

>>> from metric_learn import ITML_Supervised
>>> from sklearn.datasets import load_iris
>>> iris_data = load_iris()
>>> X = iris_data['data']
>>> Y = iris_data['target']
>>> itml = ITML_Supervised(n_constraints=200)
>>> itml.fit(X, Y)

Attributes:

bounds_numpy.ndarray, shape=(2,): Bounds on similarity, aside slack variables, s.t. d(a, b) < bounds_[0] for all given pairs of similar points a and b, and d(c, d) > bounds_[1] for all given pairs of dissimilar points c and d, with d the learned distance. If not provided at initialization, bounds_[0] and bounds_[1] are set at train time to the 5th and 95th percentile of the pairwise distances among all points in the training data X.
n_iter_int: The number of iterations the solver has run.
components_numpy.ndarray, shape=(n_features, n_features): The linear transformation L deduced from the learned Mahalanobis metric (See function components_from_metric.)

Methods

`fit`(X, y[, bounds])	Create constraints from labels and learn the ITML model.
`fit_transform`(X[, y])	Fit to data, then transform it.
`get_mahalanobis_matrix`()	Returns a copy of the Mahalanobis matrix learned by the metric learner.
`get_metadata_routing`()	Get metadata routing of this object.
`get_metric`()	Returns a function that takes as input two 1D arrays and outputs the value of the learned metric on these two points.
`get_params`([deep])	Get parameters for this estimator.
`pair_distance`(pairs)	Returns the learned Mahalanobis distance between pairs.
`pair_score`(pairs)	Returns the opposite of the learned Mahalanobis distance between pairs.
`score_pairs`(pairs)	Returns the learned Mahalanobis distance between pairs.
`set_fit_request`(*[, bounds])	Request metadata passed to the `fit` method.
`set_output`(*[, transform])	Set output container.
`set_params`(**params)	Set the parameters of this estimator.
`transform`(X)	Embeds data points in the learned linear embedding space.

__init__(gamma=1.0, max_iter=1000, tol=0.001, n_constraints=None, prior='identity', verbose=False, preprocessor=None, random_state=None, num_constraints='deprecated', convergence_threshold='deprecated')[source]

fit(X, y, bounds=None)[source]

Create constraints from labels and learn the ITML model.

Parameters:

X(n x d) matrix: Input data, where each row corresponds to a single instance.
y(n) array-like: Data labels.
boundsarray-like of two numbers: Bounds on similarity, aside slack variables, s.t. d(a, b) < bounds_[0] for all given pairs of similar points a and b, and d(c, d) > bounds_[1] for all given pairs of dissimilar points c and d, with d the learned distance. If not provided at initialization, bounds_[0] and bounds_[1] will be set to the 5th and 95th percentile of the pairwise distances among all points in the training data X.

fit_transform(X, y=None, **fit_params)

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:

Xarray-like of shape (n_samples, n_features): Input samples.
yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None: Target values (None for unsupervised transformations).
**fit_paramsdict: Additional fit parameters.

Returns:

X_newndarray array of shape (n_samples, n_features_new): Transformed array.

get_mahalanobis_matrix()

Returns a copy of the Mahalanobis matrix learned by the metric learner.

Returns:

Mnumpy.ndarray, shape=(n_features, n_features): The copy of the learned Mahalanobis matrix.

get_metadata_routing()

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest: A MetadataRequest encapsulating routing information.

get_metric()

Returns a function that takes as input two 1D arrays and outputs the value of the learned metric on these two points. Depending on the algorithm, it can return a distance or a similarity function between pairs.

This function will be independent from the metric learner that learned it (it will not be modified if the initial metric learner is modified), and it can be directly plugged into the metric argument of scikit-learn’s estimators.

Returns:

metric_funfunction: The function described above.

See also

pair_distance: a method that returns the distance between several pairs of points. Unlike get_metric, this is a method of the metric learner and therefore can change if the metric learner changes. Besides, it can use the metric learner’s preprocessor, and works on concatenated arrays.
pair_score: a method that returns the similarity score between several pairs of points. Unlike get_metric, this is a method of the metric learner and therefore can change if the metric learner changes. Besides, it can use the metric learner’s preprocessor, and works on concatenated arrays.

Examples

>>> from metric_learn import NCA
>>> from sklearn.datasets import make_classification
>>> from sklearn.neighbors import KNeighborsClassifier
>>> nca = NCA()
>>> X, y = make_classification()
>>> nca.fit(X, y)
>>> knn = KNeighborsClassifier(metric=nca.get_metric())
>>> knn.fit(X, y) 
KNeighborsClassifier(algorithm='auto', leaf_size=30,
  metric=<function MahalanobisMixin.get_metric.<locals>.metric_fun
          at 0x...>,
  metric_params=None, n_jobs=None, n_neighbors=5, p=2,
  weights='uniform')

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

pair_distance(pairs)

Returns the learned Mahalanobis distance between pairs.

This distance is defined as: $d_M(x, x') = \sqrt{(x-x')^T M (x-x')}$ where M is the learned Mahalanobis matrix, for every pair of points x and x'. This corresponds to the euclidean distance between embeddings of the points in a new space, obtained through a linear transformation. Indeed, we have also: $d_M(x, x') = \sqrt{(x_e - x_e')^T (x_e- x_e')}$, with $x_e = L x$ (See MahalanobisMixin).

Parameters:

pairsarray-like, shape=(n_pairs, 2, n_features) or (n_pairs, 2): 3D Array of pairs to score, with each row corresponding to two points, for 2D array of indices of pairs if the metric learner uses a preprocessor.

Returns:

scoresnumpy.ndarray of shape=(n_pairs,): The learned Mahalanobis distance for every pair.

See also

get_metric: a method that returns a function to compute the metric between two points. The difference with pair_distance is that it works on two 1D arrays and cannot use a preprocessor. Besides, the returned function is independent of the metric learner and hence is not modified if the metric learner is.
Mahalanobis Distances: The section of the project documentation that describes Mahalanobis Distances.

pair_score(pairs)

Returns the opposite of the learned Mahalanobis distance between pairs.

Parameters:

pairsarray-like, shape=(n_pairs, 2, n_features) or (n_pairs, 2): 3D Array of pairs to score, with each row corresponding to two points, for 2D array of indices of pairs if the metric learner uses a preprocessor.

Returns:

scoresnumpy.ndarray of shape=(n_pairs,): The opposite of the learned Mahalanobis distance for every pair.

See also

get_metric: a method that returns a function to compute the metric between two points. The difference with pair_score is that it works on two 1D arrays and cannot use a preprocessor. Besides, the returned function is independent of the metric learner and hence is not modified if the metric learner is.
Mahalanobis Distances: The section of the project documentation that describes Mahalanobis Distances.

score_pairs(pairs)

Returns the learned Mahalanobis distance between pairs.

This distance is defined as: $d_M(x, x') = \\sqrt{(x-x')^T M (x-x')}$ where M is the learned Mahalanobis matrix, for every pair of points x and x'. This corresponds to the euclidean distance between embeddings of the points in a new space, obtained through a linear transformation. Indeed, we have also: $d_M(x, x') = \\sqrt{(x_e - x_e')^T (x_e- x_e')}$, with $x_e = L x$ (See MahalanobisMixin).

Deprecated since version 0.7.0: Please use pair_distance instead.

Warning

This method will be removed in 0.8.0. Please refer to pair_distance or pair_score. This change will occur in order to add learners that don’t necessarily learn a Mahalanobis distance.

Parameters:

pairsarray-like, shape=(n_pairs, 2, n_features) or (n_pairs, 2): 3D Array of pairs to score, with each row corresponding to two points, for 2D array of indices of pairs if the metric learner uses a preprocessor.

Returns:

scoresnumpy.ndarray of shape=(n_pairs,): The learned Mahalanobis distance for every pair.

See also

get_metric: a method that returns a function to compute the metric between two points. The difference with score_pairs is that it works on two 1D arrays and cannot use a preprocessor. Besides, the returned function is independent of the metric learner and hence is not modified if the metric learner is.
Mahalanobis Distances: The section of the project documentation that describes Mahalanobis Distances.

set_fit_request(*, bounds: bool | None | str = '$UNCHANGED$') → ITML_Supervised

Request metadata passed to the fit method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config()). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

True: metadata is requested, and passed to fit if provided. The request is ignored if metadata is not provided.
False: metadata is not requested and the meta-estimator will not pass it to fit.
None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.
str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

boundsstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED: Metadata routing for bounds parameter in fit.

Returns:

selfobject: The updated object.

set_output(*, transform=None)

Set output container.

See Introducing the set_output API for an example on how to use the API.

Parameters:

transform{“default”, “pandas”}, default=None

Configure output of transform and fit_transform.

“default”: Default output format of a transformer
“pandas”: DataFrame output
None: Transform configuration is unchanged

Returns:

selfestimator instance: Estimator instance.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

transform(X)

Embeds data points in the learned linear embedding space.

Transforms samples in X into X_embedded, samples inside a new embedding space such that: X_embedded = X.dot(L.T), where L is the learned linear transformation (See MahalanobisMixin).

Parameters:

Xnumpy.ndarray, shape=(n_samples, n_features): The data points to embed.

Returns:

X_embeddednumpy.ndarray, shape=(n_samples, n_components): The embedded data points.

Examples using `metric_learn.ITML_Supervised`

Sandwich demo

Algorithms walkthrough

metric_learn.ITML_Supervised

Examples using metric_learn.ITML_Supervised

`metric_learn`.ITML_Supervised

Examples using `metric_learn.ITML_Supervised`