Group Logistic regression in python

Scikit-learn is missing a Group Logistic regression estimator. We show how to implement one with skglm.

# Author: Mathurin Massias

import numpy as np

from skglm import GeneralizedLinearEstimator
from skglm.datafits import LogisticGroup
from skglm.penalties import WeightedGroupL2
from skglm.solvers import GroupProxNewton
from skglm.utils.data import make_correlated_data, grp_converter

import matplotlib.pyplot as plt

n_features = 30
X, y, _ = make_correlated_data(
    n_samples=10, n_features=30, random_state=0)
y = np.sign(y)

Classifier creation: combination of penalty, datafit and solver.

grp_size = 3  # groups are made of groups of 3 consecutive features
n_groups = n_features // grp_size
grp_indices, grp_ptr = grp_converter(grp_size, n_features=n_features)
alpha = 0.01
weights = np.ones(n_groups)
penalty = WeightedGroupL2(alpha, weights, grp_ptr, grp_indices)
datafit = LogisticGroup(grp_ptr, grp_indices)
solver = GroupProxNewton(verbose=2)

Train the model

clf = GeneralizedLinearEstimator(datafit, penalty, solver)
clf.fit(X, y)

Iteration 1: 0.6931471806, stopping crit: 5.93e-01
PN iteration 1: 0.1828438632, stopping crit in: 1.48e-01
Early exit
Iteration 2: 0.1828438632, stopping crit: 1.48e-01
PN iteration 1: 0.1122823448, stopping crit in: 4.83e-02
PN iteration 2: 0.0920730009, stopping crit in: 1.56e-02
Early exit
Iteration 3: 0.0920730009, stopping crit: 1.56e-02
PN iteration 1: 0.0849753666, stopping crit in: 5.98e-03
PN iteration 2: 0.0799335206, stopping crit in: 1.74e-03
Early exit
Iteration 4: 0.0799335206, stopping crit: 1.74e-03
PN iteration 1: 0.0794189783, stopping crit in: 2.10e-04
Early exit
Iteration 5: 0.0794189783, stopping crit: 2.10e-04
PN iteration 1: 0.0794086709, stopping crit in: 6.08e-05
Early exit
Iteration 6: 0.0794086709, stopping crit: 6.08e-05

GeneralizedLinearEstimator(datafit=LogisticGroup, penalty=WeightedGroupL2, alpha=0.01)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Fit check that groups are either all 0 or all non zero

print(clf.coef_.reshape(-1, grp_size))

[[ 0.          0.          0.        ]
 [-1.09358498 -0.88830458 -0.77241873]
 [-1.68346202 -1.26329232 -1.04960499]
 [-0.16612516  0.0249733  -0.03614162]
 [ 0.          0.          0.        ]
 [-0.01611123 -0.01500223 -0.00637489]
 [-0.9086726  -0.95978761 -0.49653568]
 [ 0.          0.          0.        ]
 [ 0.          0.          0.        ]
 [ 0.57186315 -0.24696147  0.16123249]]

Visualise group-level sparsity

coef_by_group = clf.coef_.reshape(-1, grp_size)
group_norms = np.linalg.norm(coef_by_group, axis=1)

plt.figure(figsize=(8, 4))
plt.bar(np.arange(n_groups), group_norms)
plt.xlabel("Group index")
plt.ylabel("L2 norm of coefficients")
plt.title("Group Sparsity Pattern")
plt.tight_layout()
plt.show()

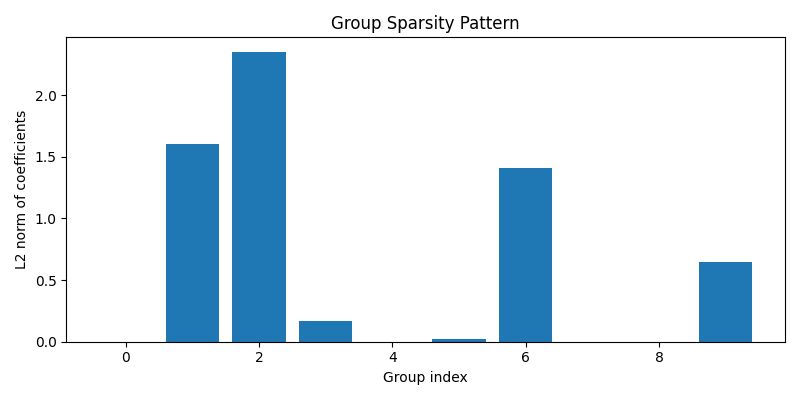
This plot shows the L2 norm of the coefficients for each group. Groups with a zero norm have been set inactive by the model, illustrating how Group Logistic Regression enforces sparsity at the group level. (Note: This example uses a tiny synthetic dataset, so the pattern has limited interpretability.)